Certification Courses

Created with over a decade of experience and thousands of feedback.

Learn Python

Learn HTML

Learn JavaScript

Learn SQL

Learn DSA

View all Courses on

Learn C

Learn C++

Learn Java

AVL Tree

AVL tree is a self-balancing binary search tree in which each node maintains extra information called a balance factor whose value is either -1, 0 or +1.

AVL tree got its name after its inventor Georgy Adelson-Velsky and Landis.

Balance Factor

Balance factor of a node in an AVL tree is the difference between the height of the left subtree and that of the right subtree of that node.

Balance Factor = (Height of Left Subtree - Height of Right Subtree) or (Height of Right Subtree - Height of Left Subtree)

The self balancing property of an avl tree is maintained by the balance factor. The value of balance factor should always be -1, 0 or +1.

An example of a balanced avl tree is:

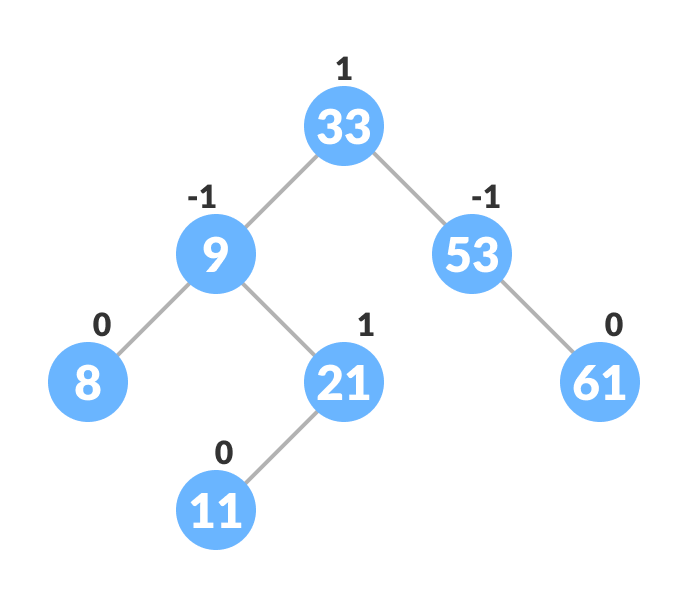
Operations on an AVL tree

Various operations that can be performed on an AVL tree are:

Rotating the subtrees in an AVL Tree

In rotation operation, the positions of the nodes of a subtree are interchanged.

There are two types of rotations:

Left Rotate

In left-rotation, the arrangement of the nodes on the right is transformed into the arrangements on the left node.

Algorithm

Let the initial tree be:

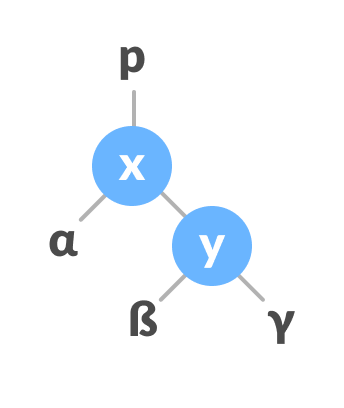
Left rotate
If y has a left subtree, assign x as the parent of the left subtree of y.

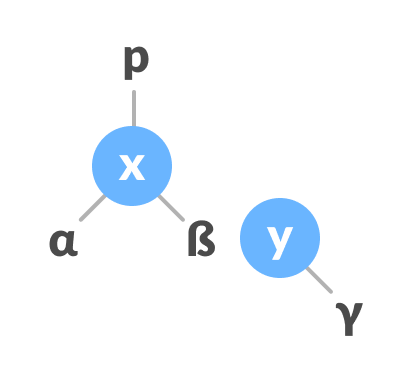
Assign x as the parent of the left subtree of y
If the parent of x is NULL, make y as the root of the tree.
Else if x is the left child of p, make y as the left child of p.
Else assign y as the right child of p.

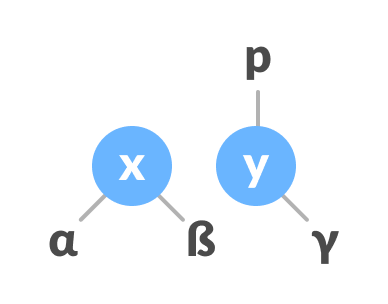
Change the parent of x to that of y
Make y as the parent of x.

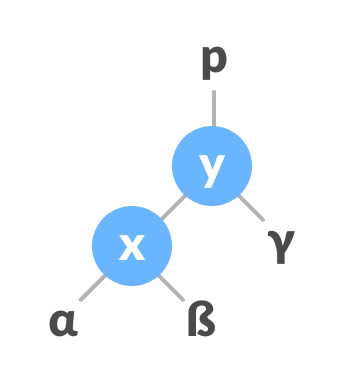
Assign y as the parent of x.

Right Rotate

In right-rotation, the arrangement of the nodes on the left is transformed into the arrangements on the right node.

Let the initial tree be:

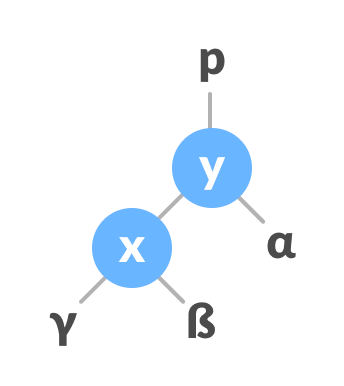
Initial tree
If x has a right subtree, assign y as the parent of the right subtree of x.

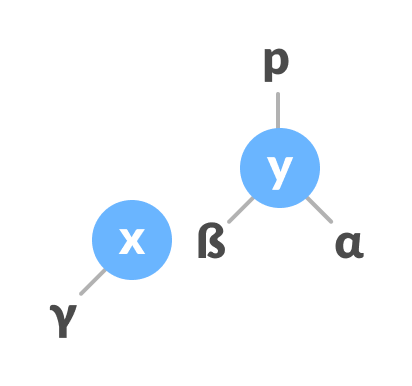
Assign y as the parent of the right subtree of x
If the parent of y is NULL, make x as the root of the tree.
Else if y is the right child of its parent p, make x as the right child of p.
Else assign x as the left child of p.

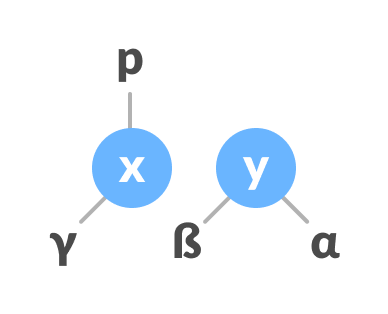
Assign the parent of y as the parent of x.
Make x as the parent of y.

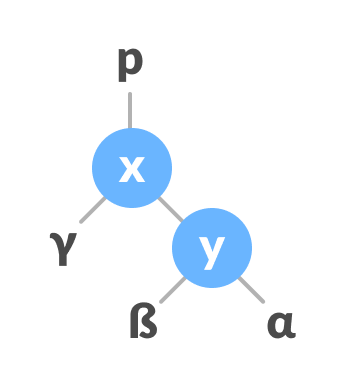
Assign x as the parent of y

Left-Right and Right-Left Rotate

In left-right rotation, the arrangements are first shifted to the left and then to the right.

Do left rotation on x-y.

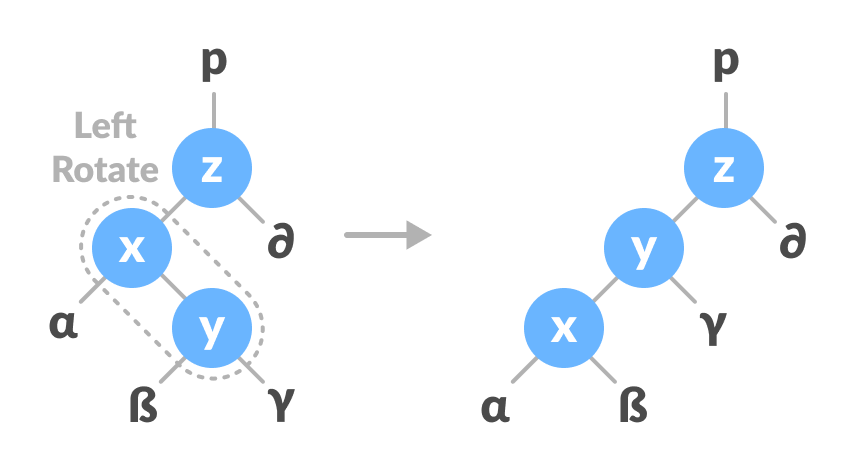
Left rotate x-y
Do right rotation on y-z.

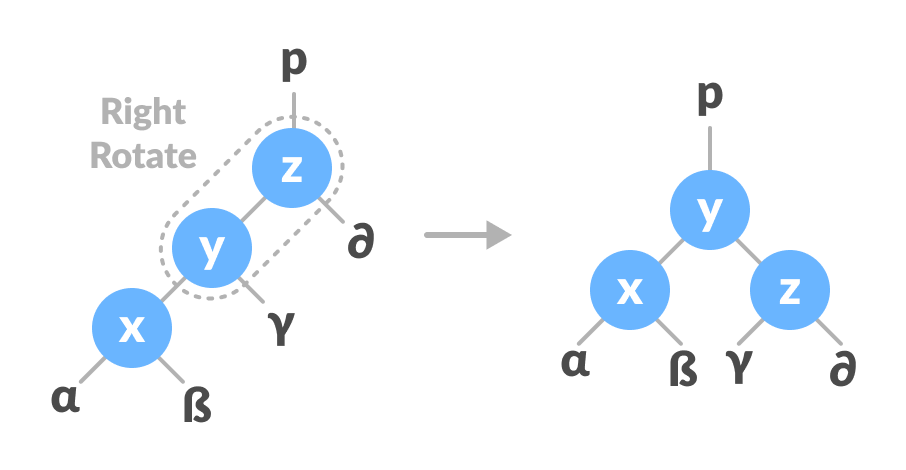
Right rotate z-y

In right-left rotation, the arrangements are first shifted to the right and then to the left.

Do right rotation on x-y.

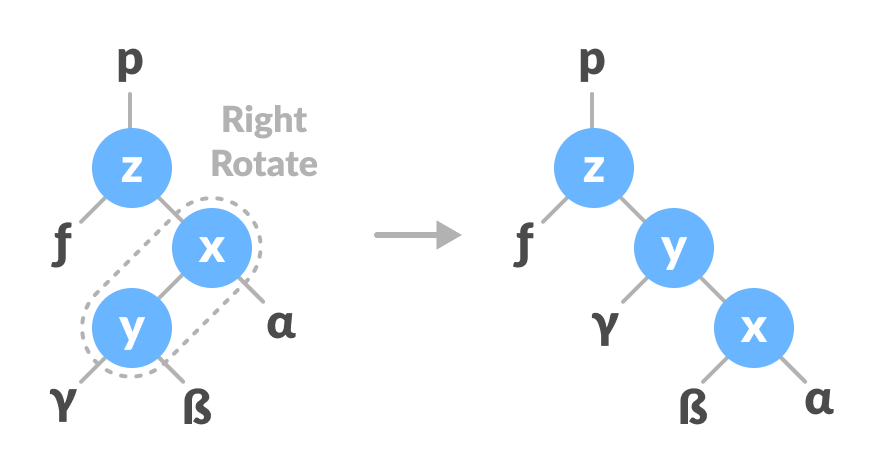
Right rotate x-y
Do left rotation on z-y.

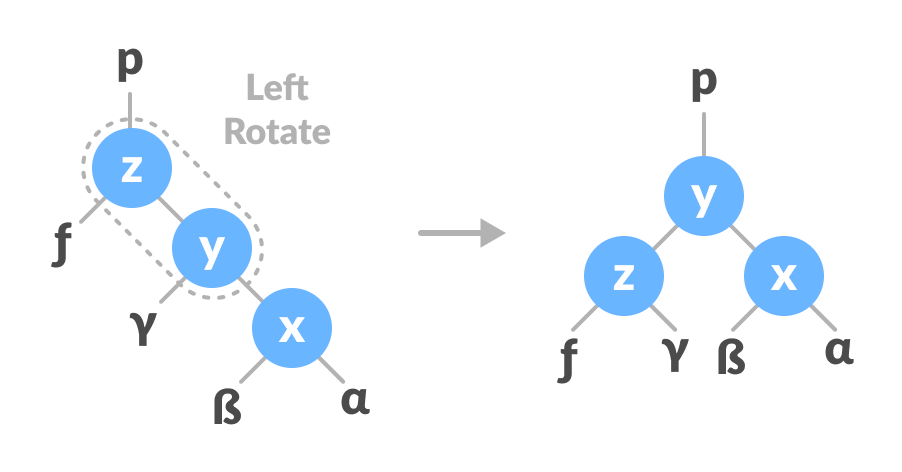
Left rotate z-y

Algorithm to insert a newNode

A newNode is always inserted as a leaf node with balance factor equal to 0.

Let the initial tree be:

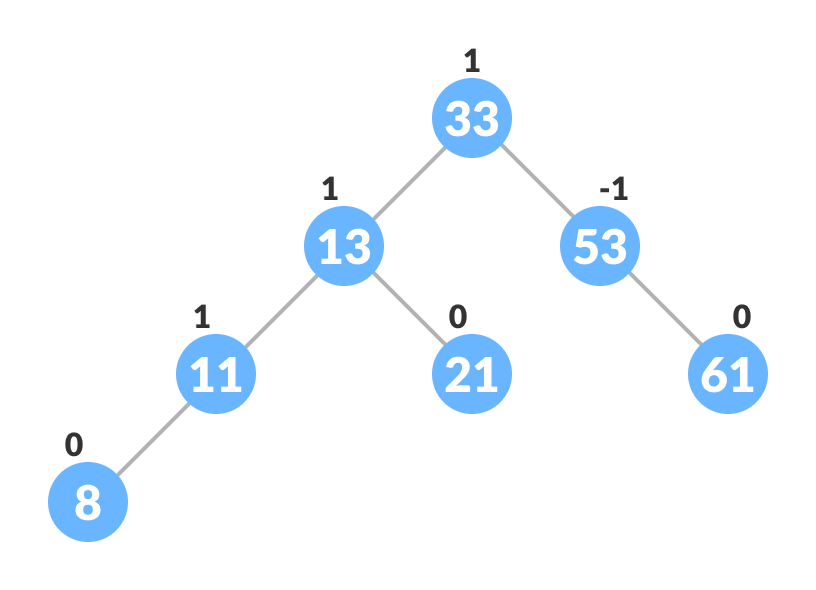
Initial tree for insertion

Let the node to be inserted be:

New node
Go to the appropriate leaf node to insert a newNode using the following recursive steps. Compare newKey with rootKey of the current tree.
1. If newKey < rootKey, call insertion algorithm on the left subtree of the current node until the leaf node is reached.
2. Else if newKey > rootKey, call insertion algorithm on the right subtree of current node until the leaf node is reached.
3. Else, return leafNode.
  
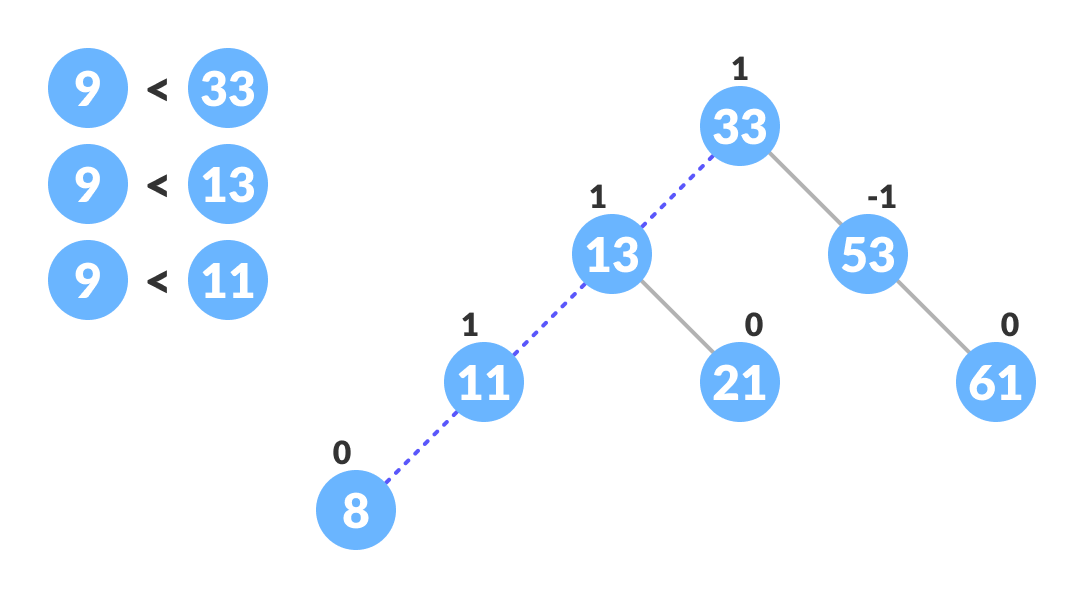
  Finding the location to insert newNode
Compare leafKey obtained from the above steps with newKey:
1. If newKey < leafKey, make newNode as the leftChild of leafNode.
2. Else, make newNode as rightChild of leafNode.
  
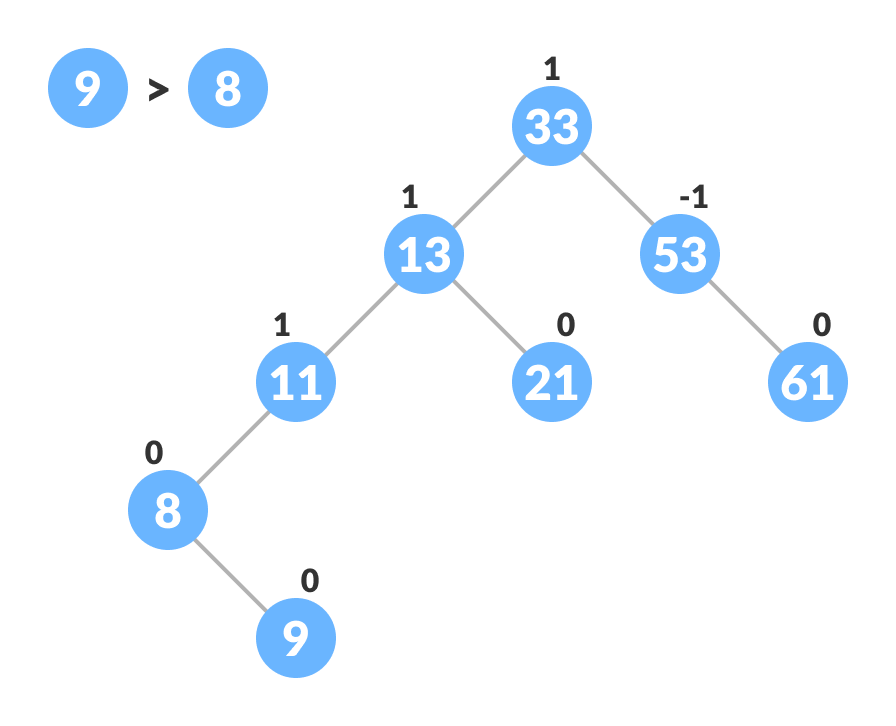
  Inserting the new node
Update balanceFactor of the nodes.

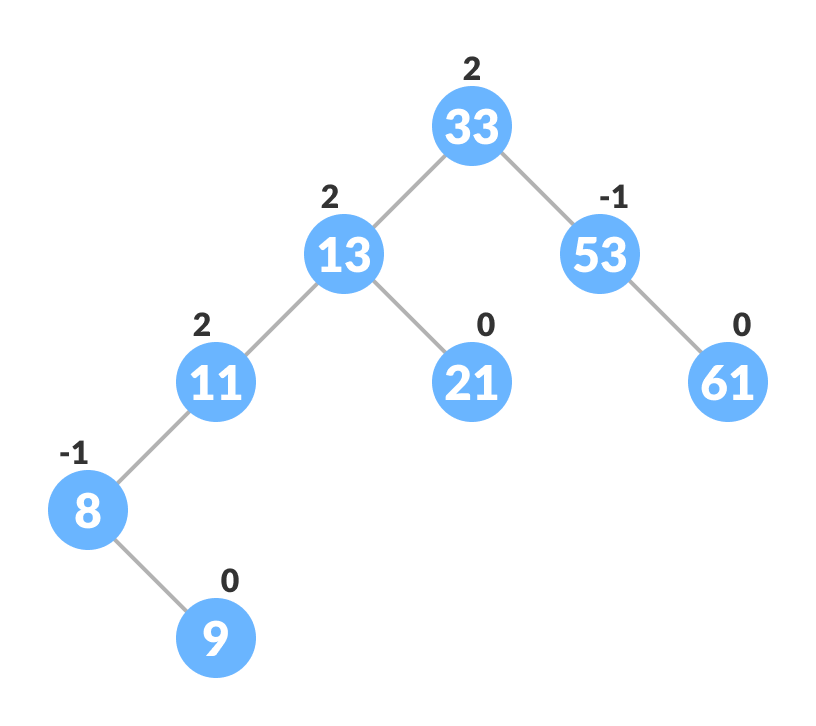
Updating the balance factor after insertion
If the nodes are unbalanced, then rebalance the node.
1. If balanceFactor > 1, it means the height of the left subtree is greater than that of the right subtree. So, do a right rotation or left-right rotation
  1. If newNodeKey < leftChildKey do right rotation.
  2. Else, do left-right rotation.
    
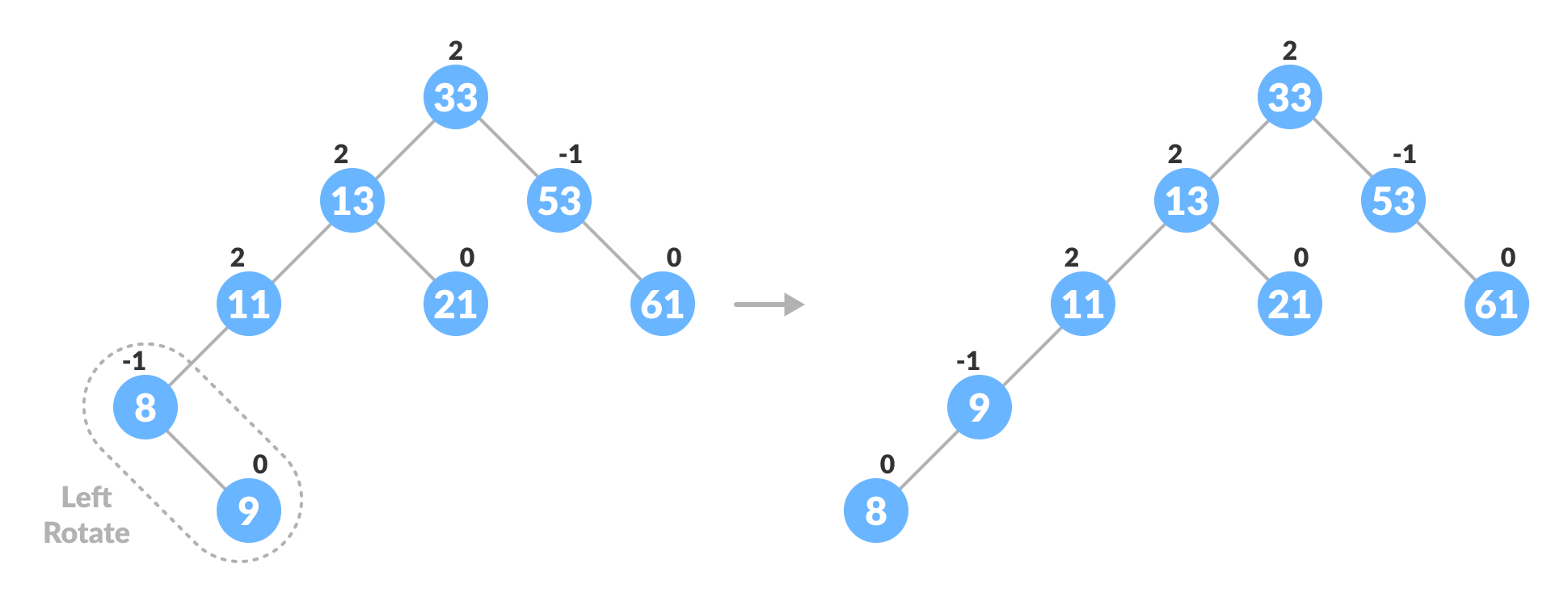
    Balancing the tree with rotation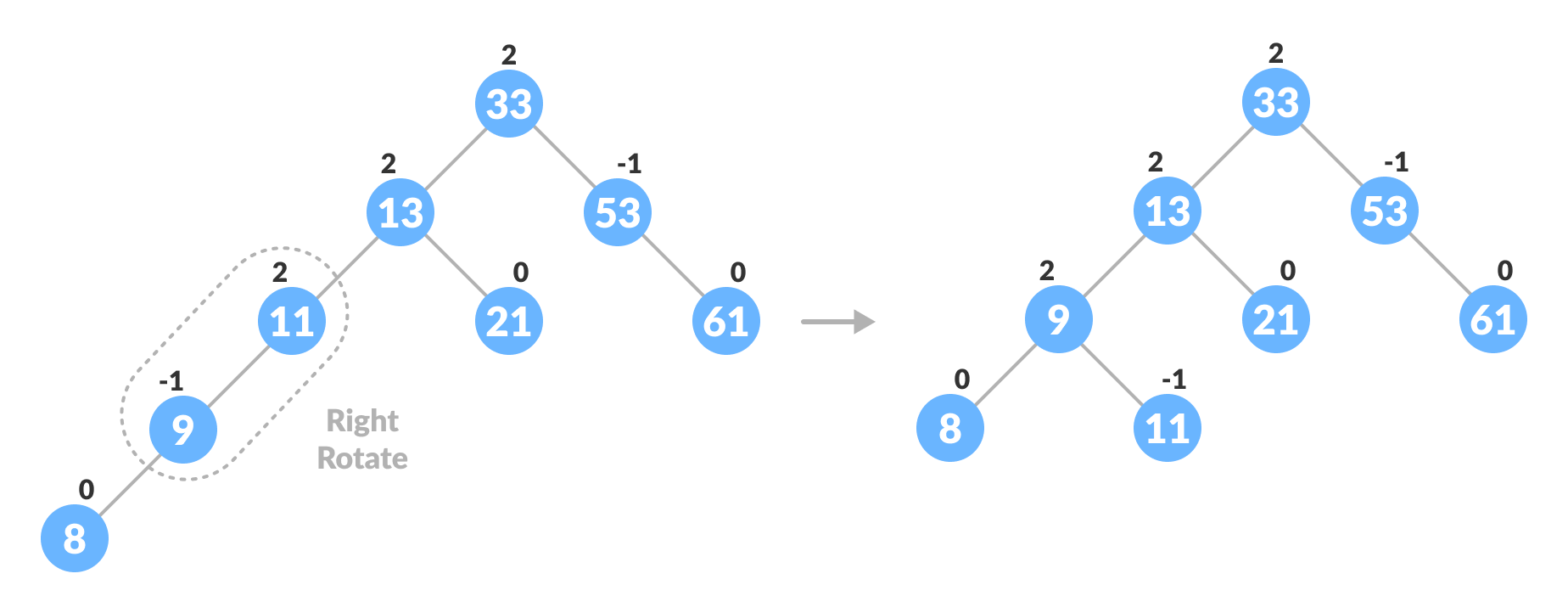
    
    Balancing the tree with rotation
2. If balanceFactor < -1, it means the height of the right subtree is greater than that of the left subtree. So, do right rotation or right-left rotation
  1. If newNodeKey > rightChildKey do left rotation.
  2. Else, do right-left rotation
The final tree is:

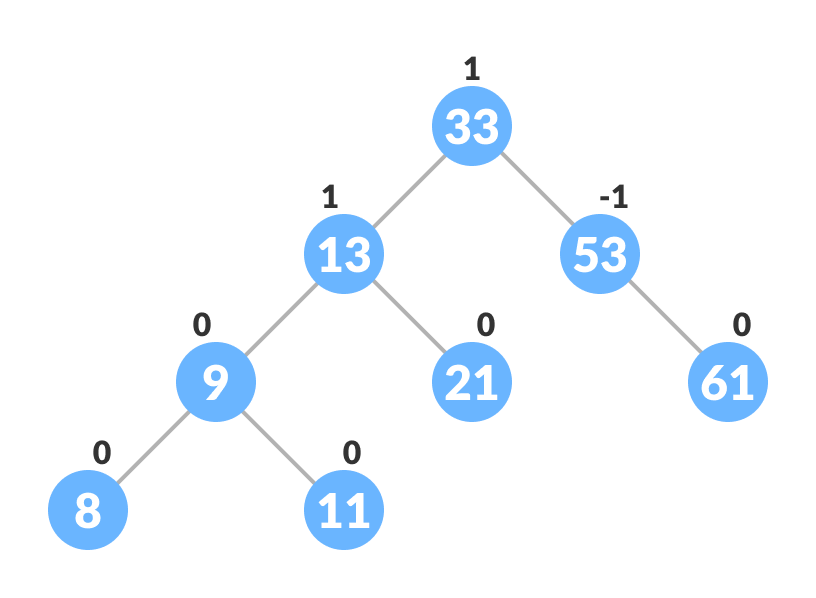
Final balanced tree

Algorithm to Delete a node

A node is always deleted as a leaf node. After deleting a node, the balance factors of the nodes get changed. In order to rebalance the balance factor, suitable rotations are performed.

Locate nodeToBeDeleted (recursion is used to find nodeToBeDeleted in the code used below).

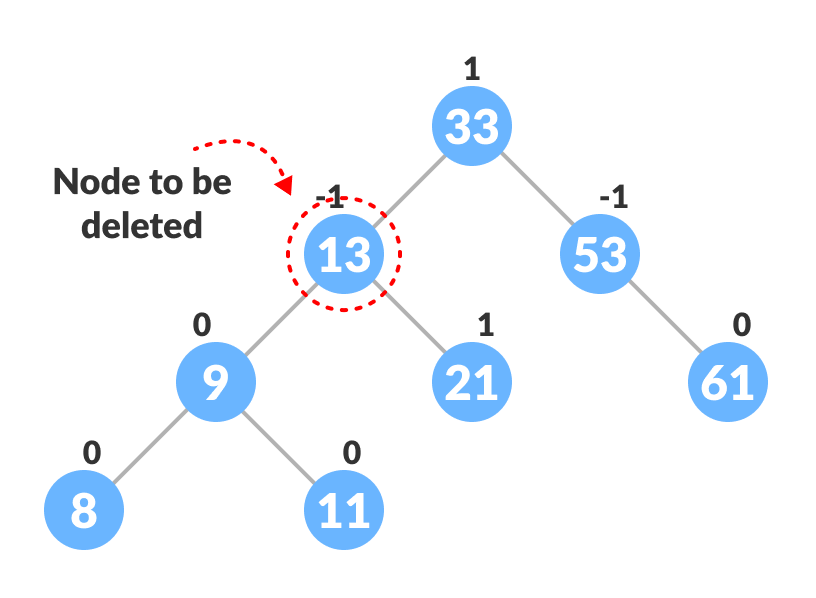
Locating the node to be deleted
There are three cases for deleting a node:
1. If nodeToBeDeleted is the leaf node (ie. does not have any child), then remove nodeToBeDeleted.
2. If nodeToBeDeleted has one child, then substitute the contents of nodeToBeDeleted with that of the child. Remove the child.
3. If nodeToBeDeleted has two children, find the inorder successor w of nodeToBeDeleted (ie. node with a minimum value of key in the right subtree).
  
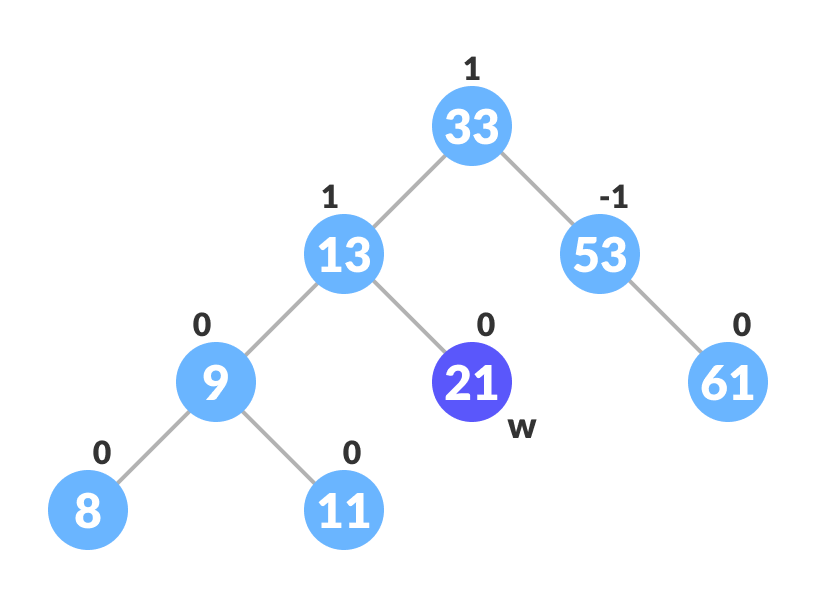
  Finding the successor
  1. Substitute the contents of nodeToBeDeleted with that of w.
    
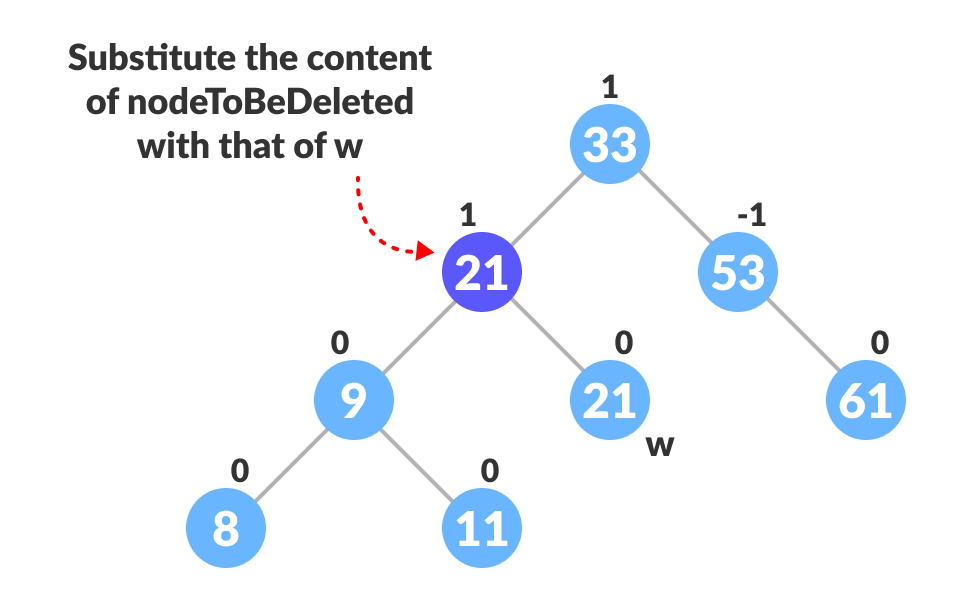
    Substitute the node to be deleted
  2. Remove the leaf node w.
    
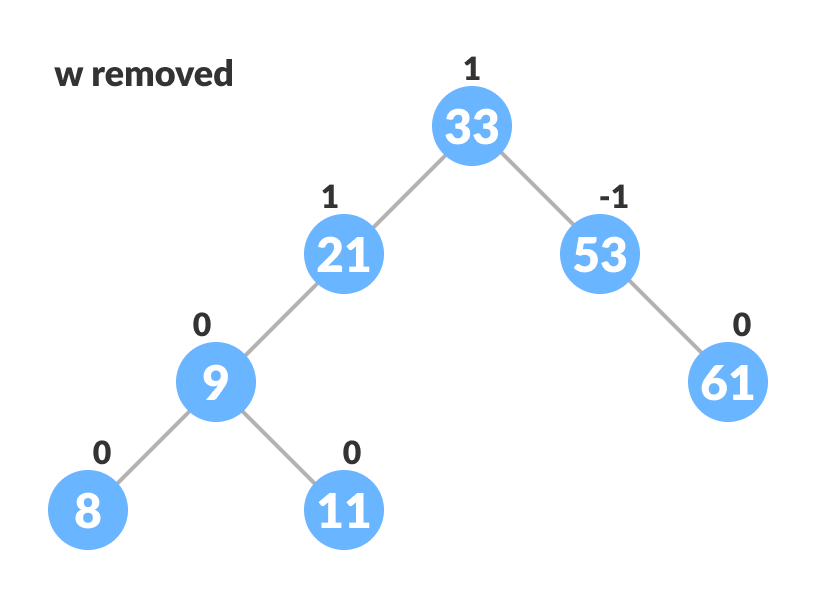
    Remove w
Update balanceFactor of the nodes.

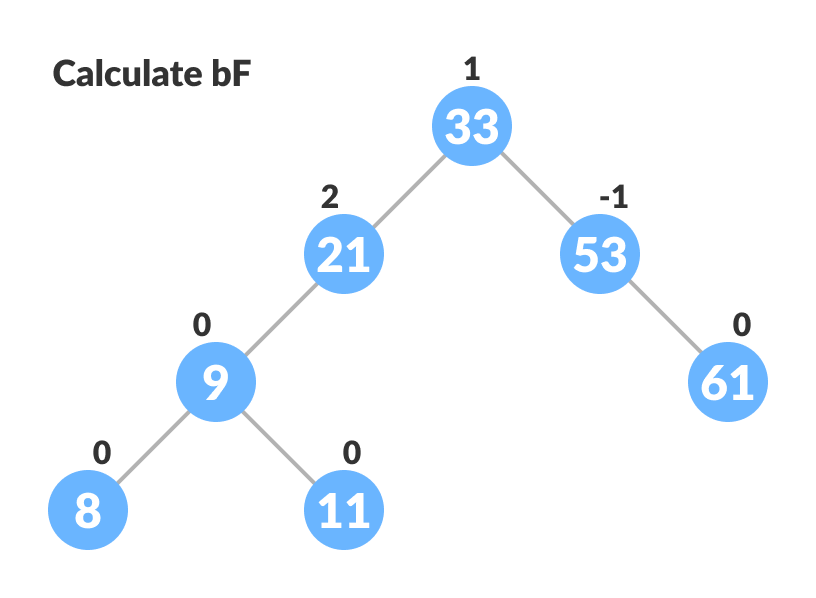
Update bf
Rebalance the tree if the balance factor of any of the nodes is not equal to -1, 0 or 1.
1. If balanceFactor of currentNode > 1,
  1. If balanceFactor of leftChild >= 0, do right rotation.
    
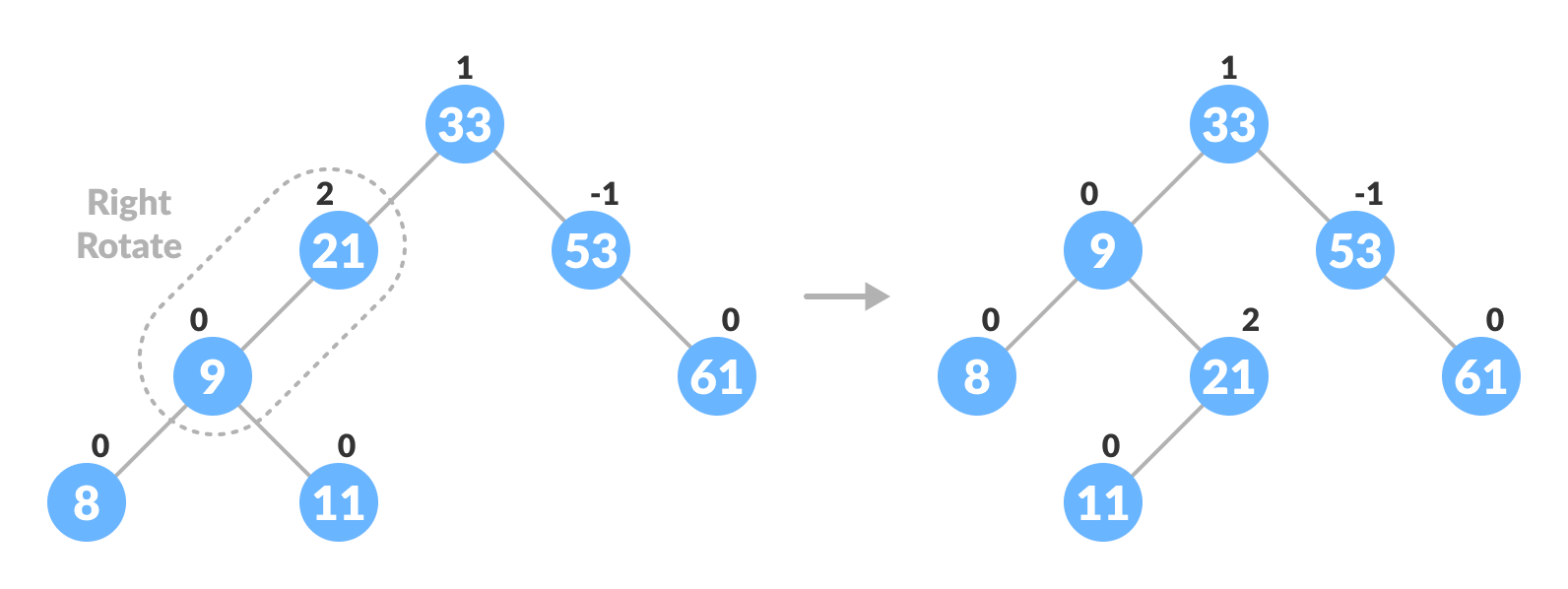
    Right-rotate for balancing the tree
  2. Else do left-right rotation.
2. If balanceFactor of currentNode < -1,
  1. If balanceFactor of rightChild <= 0, do left rotation.
  2. Else do right-left rotation.
The final tree is:

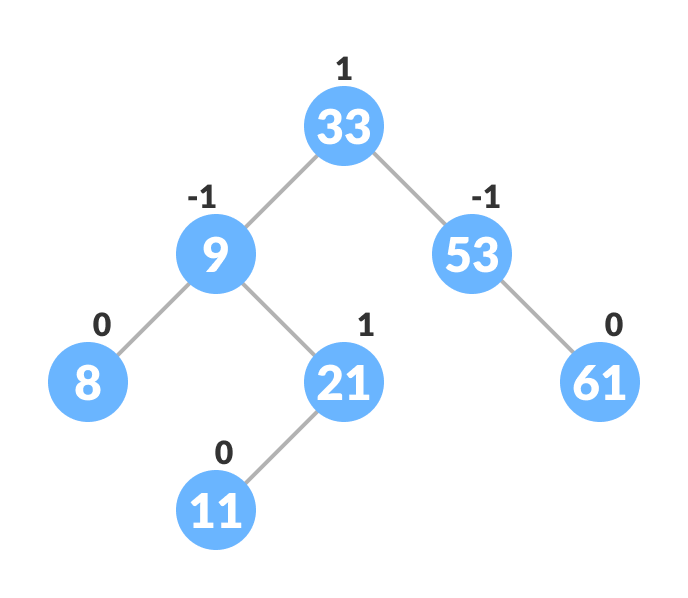
Avl tree final

Python, Java and C/C++ Examples

Python

Java

C++

# AVL tree implementation in Python


import sys

# Create a tree node
class TreeNode(object):
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.height = 1


class AVLTree(object):

    # Function to insert a node
    def insert_node(self, root, key):

        # Find the correct location and insert the node
        if not root:
            return TreeNode(key)
        elif key < root.key:
            root.left = self.insert_node(root.left, key)
        else:
            root.right = self.insert_node(root.right, key)

        root.height = 1 + max(self.getHeight(root.left),
                              self.getHeight(root.right))

        # Update the balance factor and balance the tree
        balanceFactor = self.getBalance(root)
        if balanceFactor > 1:
            if key < root.left.key:
                return self.rightRotate(root)
            else:
                root.left = self.leftRotate(root.left)
                return self.rightRotate(root)

        if balanceFactor < -1:
            if key > root.right.key:
                return self.leftRotate(root)
            else:
                root.right = self.rightRotate(root.right)
                return self.leftRotate(root)

        return root

    # Function to delete a node
    def delete_node(self, root, key):

        # Find the node to be deleted and remove it
        if not root:
            return root
        elif key < root.key:
            root.left = self.delete_node(root.left, key)
        elif key > root.key:
            root.right = self.delete_node(root.right, key)
        else:
            if root.left is None:
                temp = root.right
                root = None
                return temp
            elif root.right is None:
                temp = root.left
                root = None
                return temp
            temp = self.getMinValueNode(root.right)
            root.key = temp.key
            root.right = self.delete_node(root.right,
                                          temp.key)
        if root is None:
            return root

        # Update the balance factor of nodes
        root.height = 1 + max(self.getHeight(root.left),
                              self.getHeight(root.right))

        balanceFactor = self.getBalance(root)

        # Balance the tree
        if balanceFactor > 1:
            if self.getBalance(root.left) >= 0:
                return self.rightRotate(root)
            else:
                root.left = self.leftRotate(root.left)
                return self.rightRotate(root)
        if balanceFactor < -1:
            if self.getBalance(root.right) <= 0:
                return self.leftRotate(root)
            else:
                root.right = self.rightRotate(root.right)
                return self.leftRotate(root)
        return root

    # Function to perform left rotation
    def leftRotate(self, z):
        y = z.right
        T2 = y.left
        y.left = z
        z.right = T2
        z.height = 1 + max(self.getHeight(z.left),
                           self.getHeight(z.right))
        y.height = 1 + max(self.getHeight(y.left),
                           self.getHeight(y.right))
        return y

    # Function to perform right rotation
    def rightRotate(self, z):
        y = z.left
        T3 = y.right
        y.right = z
        z.left = T3
        z.height = 1 + max(self.getHeight(z.left),
                           self.getHeight(z.right))
        y.height = 1 + max(self.getHeight(y.left),
                           self.getHeight(y.right))
        return y

    # Get the height of the node
    def getHeight(self, root):
        if not root:
            return 0
        return root.height

    # Get balance factore of the node
    def getBalance(self, root):
        if not root:
            return 0
        return self.getHeight(root.left) - self.getHeight(root.right)

    def getMinValueNode(self, root):
        if root is None or root.left is None:
            return root
        return self.getMinValueNode(root.left)

    def preOrder(self, root):
        if not root:
            return
        print("{0} ".format(root.key), end="")
        self.preOrder(root.left)
        self.preOrder(root.right)

    # Print the tree
    def printHelper(self, currPtr, indent, last):
        if currPtr != None:
            sys.stdout.write(indent)
            if last:
                sys.stdout.write("R----")
                indent += "     "
            else:
                sys.stdout.write("L----")
                indent += "|    "
            print(currPtr.key)
            self.printHelper(currPtr.left, indent, False)
            self.printHelper(currPtr.right, indent, True)


myTree = AVLTree()
root = None
nums = [33, 13, 52, 9, 21, 61, 8, 11]
for num in nums:
    root = myTree.insert_node(root, num)
myTree.printHelper(root, "", True)
key = 13
root = myTree.delete_node(root, key)
print("After Deletion: ")
myTree.printHelper(root, "", True)

// AVL tree implementation in Java

// Create node
class Node {
  int item, height;
  Node left, right;

  Node(int d) {
    item = d;
    height = 1;
  }
}

// Tree class
class AVLTree {
  Node root;

  int height(Node N) {
    if (N == null)
      return 0;
    return N.height;
  }

  int max(int a, int b) {
    return (a > b) ? a : b;
  }

  Node rightRotate(Node y) {
    Node x = y.left;
    Node T2 = x.right;
    x.right = y;
    y.left = T2;
    y.height = max(height(y.left), height(y.right)) + 1;
    x.height = max(height(x.left), height(x.right)) + 1;
    return x;
  }

  Node leftRotate(Node x) {
    Node y = x.right;
    Node T2 = y.left;
    y.left = x;
    x.right = T2;
    x.height = max(height(x.left), height(x.right)) + 1;
    y.height = max(height(y.left), height(y.right)) + 1;
    return y;
  }

  // Get balance factor of a node
  int getBalanceFactor(Node N) {
    if (N == null)
      return 0;
    return height(N.left) - height(N.right);
  }

  // Insert a node
  Node insertNode(Node node, int item) {

    // Find the position and insert the node
    if (node == null)
      return (new Node(item));
    if (item < node.item)
      node.left = insertNode(node.left, item);
    else if (item > node.item)
      node.right = insertNode(node.right, item);
    else
      return node;

    // Update the balance factor of each node
    // And, balance the tree
    node.height = 1 + max(height(node.left), height(node.right));
    int balanceFactor = getBalanceFactor(node);
    if (balanceFactor > 1) {
      if (item < node.left.item) {
        return rightRotate(node);
      } else if (item > node.left.item) {
        node.left = leftRotate(node.left);
        return rightRotate(node);
      }
    }
    if (balanceFactor < -1) {
      if (item > node.right.item) {
        return leftRotate(node);
      } else if (item < node.right.item) {
        node.right = rightRotate(node.right);
        return leftRotate(node);
      }
    }
    return node;
  }

  Node nodeWithMimumValue(Node node) {
    Node current = node;
    while (current.left != null)
      current = current.left;
    return current;
  }

  // Delete a node
  Node deleteNode(Node root, int item) {

    // Find the node to be deleted and remove it
    if (root == null)
      return root;
    if (item < root.item)
      root.left = deleteNode(root.left, item);
    else if (item > root.item)
      root.right = deleteNode(root.right, item);
    else {
      if ((root.left == null) || (root.right == null)) {
        Node temp = null;
        if (temp == root.left)
          temp = root.right;
        else
          temp = root.left;
        if (temp == null) {
          temp = root;
          root = null;
        } else
          root = temp;
      } else {
        Node temp = nodeWithMimumValue(root.right);
        root.item = temp.item;
        root.right = deleteNode(root.right, temp.item);
      }
    }
    if (root == null)
      return root;

    // Update the balance factor of each node and balance the tree
    root.height = max(height(root.left), height(root.right)) + 1;
    int balanceFactor = getBalanceFactor(root);
    if (balanceFactor > 1) {
      if (getBalanceFactor(root.left) >= 0) {
        return rightRotate(root);
      } else {
        root.left = leftRotate(root.left);
        return rightRotate(root);
      }
    }
    if (balanceFactor < -1) {
      if (getBalanceFactor(root.right) <= 0) {
        return leftRotate(root);
      } else {
        root.right = rightRotate(root.right);
        return leftRotate(root);
      }
    }
    return root;
  }

  void preOrder(Node node) {
    if (node != null) {
      System.out.print(node.item + " ");
      preOrder(node.left);
      preOrder(node.right);
    }
  }

  // Print the tree
  private void printTree(Node currPtr, String indent, boolean last) {
    if (currPtr != null) {
      System.out.print(indent);
      if (last) {
        System.out.print("R----");
        indent += "   ";
      } else {
        System.out.print("L----");
        indent += "|  ";
      }
      System.out.println(currPtr.item);
      printTree(currPtr.left, indent, false);
      printTree(currPtr.right, indent, true);
    }
  }

  // Driver code
  public static void main(String[] args) {
    AVLTree tree = new AVLTree();
    tree.root = tree.insertNode(tree.root, 33);
    tree.root = tree.insertNode(tree.root, 13);
    tree.root = tree.insertNode(tree.root, 53);
    tree.root = tree.insertNode(tree.root, 9);
    tree.root = tree.insertNode(tree.root, 21);
    tree.root = tree.insertNode(tree.root, 61);
    tree.root = tree.insertNode(tree.root, 8);
    tree.root = tree.insertNode(tree.root, 11);
    tree.printTree(tree.root, "", true);
    tree.root = tree.deleteNode(tree.root, 13);
    System.out.println("After Deletion: ");
    tree.printTree(tree.root, "", true);
  }
}

// AVL tree implementation in C

#include <stdio.h>
#include <stdlib.h>

// Create Node
struct Node {
  int key;
  struct Node *left;
  struct Node *right;
  int height;
};

int max(int a, int b);

// Calculate height
int height(struct Node *N) {
  if (N == NULL)
    return 0;
  return N->height;
}

int max(int a, int b) {
  return (a > b) ? a : b;
}

// Create a node
struct Node *newNode(int key) {
  struct Node *node = (struct Node *)
    malloc(sizeof(struct Node));
  node->key = key;
  node->left = NULL;
  node->right = NULL;
  node->height = 1;
  return (node);
}

// Right rotate
struct Node *rightRotate(struct Node *y) {
  struct Node *x = y->left;
  struct Node *T2 = x->right;

  x->right = y;
  y->left = T2;

  y->height = max(height(y->left), height(y->right)) + 1;
  x->height = max(height(x->left), height(x->right)) + 1;

  return x;
}

// Left rotate
struct Node *leftRotate(struct Node *x) {
  struct Node *y = x->right;
  struct Node *T2 = y->left;

  y->left = x;
  x->right = T2;

  x->height = max(height(x->left), height(x->right)) + 1;
  y->height = max(height(y->left), height(y->right)) + 1;

  return y;
}

// Get the balance factor
int getBalance(struct Node *N) {
  if (N == NULL)
    return 0;
  return height(N->left) - height(N->right);
}

// Insert node
struct Node *insertNode(struct Node *node, int key) {
  // Find the correct position to insertNode the node and insertNode it
  if (node == NULL)
    return (newNode(key));

  if (key < node->key)
    node->left = insertNode(node->left, key);
  else if (key > node->key)
    node->right = insertNode(node->right, key);
  else
    return node;

  // Update the balance factor of each node and
  // Balance the tree
  node->height = 1 + max(height(node->left),
               height(node->right));

  int balance = getBalance(node);
  if (balance > 1 && key < node->left->key)
    return rightRotate(node);

  if (balance < -1 && key > node->right->key)
    return leftRotate(node);

  if (balance > 1 && key > node->left->key) {
    node->left = leftRotate(node->left);
    return rightRotate(node);
  }

  if (balance < -1 && key < node->right->key) {
    node->right = rightRotate(node->right);
    return leftRotate(node);
  }

  return node;
}

struct Node *minValueNode(struct Node *node) {
  struct Node *current = node;

  while (current->left != NULL)
    current = current->left;

  return current;
}

// Delete a nodes
struct Node *deleteNode(struct Node *root, int key) {
  // Find the node and delete it
  if (root == NULL)
    return root;

  if (key < root->key)
    root->left = deleteNode(root->left, key);

  else if (key > root->key)
    root->right = deleteNode(root->right, key);

  else {
    if ((root->left == NULL) || (root->right == NULL)) {
      struct Node *temp = root->left ? root->left : root->right;

      if (temp == NULL) {
        temp = root;
        root = NULL;
      } else
        *root = *temp;
      free(temp);
    } else {
      struct Node *temp = minValueNode(root->right);

      root->key = temp->key;

      root->right = deleteNode(root->right, temp->key);
    }
  }

  if (root == NULL)
    return root;

  // Update the balance factor of each node and
  // balance the tree
  root->height = 1 + max(height(root->left),
               height(root->right));

  int balance = getBalance(root);
  if (balance > 1 && getBalance(root->left) >= 0)
    return rightRotate(root);

  if (balance > 1 && getBalance(root->left) < 0) {
    root->left = leftRotate(root->left);
    return rightRotate(root);
  }

  if (balance < -1 && getBalance(root->right) <= 0)
    return leftRotate(root);

  if (balance < -1 && getBalance(root->right) > 0) {
    root->right = rightRotate(root->right);
    return leftRotate(root);
  }

  return root;
}

// Print the tree
void printPreOrder(struct Node *root) {
  if (root != NULL) {
    printf("%d ", root->key);
    printPreOrder(root->left);
    printPreOrder(root->right);
  }
}

int main() {
  struct Node *root = NULL;

  root = insertNode(root, 2);
  root = insertNode(root, 1);
  root = insertNode(root, 7);
  root = insertNode(root, 4);
  root = insertNode(root, 5);
  root = insertNode(root, 3);
  root = insertNode(root, 8);

  printPreOrder(root);

  root = deleteNode(root, 3);

  printf("\nAfter deletion: ");
  printPreOrder(root);

  return 0;
}

// AVL tree implementation in C++

#include <iostream>
using namespace std;

class Node {
   public:
  int key;
  Node *left;
  Node *right;
  int height;
};

int max(int a, int b);

// Calculate height
int height(Node *N) {
  if (N == NULL)
    return 0;
  return N->height;
}

int max(int a, int b) {
  return (a > b) ? a : b;
}

// New node creation
Node *newNode(int key) {
  Node *node = new Node();
  node->key = key;
  node->left = NULL;
  node->right = NULL;
  node->height = 1;
  return (node);
}

// Rotate right
Node *rightRotate(Node *y) {
  Node *x = y->left;
  Node *T2 = x->right;
  x->right = y;
  y->left = T2;
  y->height = max(height(y->left),
          height(y->right)) +
        1;
  x->height = max(height(x->left),
          height(x->right)) +
        1;
  return x;
}

// Rotate left
Node *leftRotate(Node *x) {
  Node *y = x->right;
  Node *T2 = y->left;
  y->left = x;
  x->right = T2;
  x->height = max(height(x->left),
          height(x->right)) +
        1;
  y->height = max(height(y->left),
          height(y->right)) +
        1;
  return y;
}

// Get the balance factor of each node
int getBalanceFactor(Node *N) {
  if (N == NULL)
    return 0;
  return height(N->left) -
       height(N->right);
}

// Insert a node
Node *insertNode(Node *node, int key) {
  // Find the correct postion and insert the node
  if (node == NULL)
    return (newNode(key));
  if (key < node->key)
    node->left = insertNode(node->left, key);
  else if (key > node->key)
    node->right = insertNode(node->right, key);
  else
    return node;

  // Update the balance factor of each node and
  // balance the tree
  node->height = 1 + max(height(node->left),
               height(node->right));
  int balanceFactor = getBalanceFactor(node);
  if (balanceFactor > 1) {
    if (key < node->left->key) {
      return rightRotate(node);
    } else if (key > node->left->key) {
      node->left = leftRotate(node->left);
      return rightRotate(node);
    }
  }
  if (balanceFactor < -1) {
    if (key > node->right->key) {
      return leftRotate(node);
    } else if (key < node->right->key) {
      node->right = rightRotate(node->right);
      return leftRotate(node);
    }
  }
  return node;
}

// Node with minimum value
Node *nodeWithMimumValue(Node *node) {
  Node *current = node;
  while (current->left != NULL)
    current = current->left;
  return current;
}

// Delete a node
Node *deleteNode(Node *root, int key) {
  // Find the node and delete it
  if (root == NULL)
    return root;
  if (key < root->key)
    root->left = deleteNode(root->left, key);
  else if (key > root->key)
    root->right = deleteNode(root->right, key);
  else {
    if ((root->left == NULL) ||
      (root->right == NULL)) {
      Node *temp = root->left ? root->left : root->right;
      if (temp == NULL) {
        temp = root;
        root = NULL;
      } else
        *root = *temp;
      free(temp);
    } else {
      Node *temp = nodeWithMimumValue(root->right);
      root->key = temp->key;
      root->right = deleteNode(root->right,
                   temp->key);
    }
  }

  if (root == NULL)
    return root;

  // Update the balance factor of each node and
  // balance the tree
  root->height = 1 + max(height(root->left),
               height(root->right));
  int balanceFactor = getBalanceFactor(root);
  if (balanceFactor > 1) {
    if (getBalanceFactor(root->left) >= 0) {
      return rightRotate(root);
    } else {
      root->left = leftRotate(root->left);
      return rightRotate(root);
    }
  }
  if (balanceFactor < -1) {
    if (getBalanceFactor(root->right) <= 0) {
      return leftRotate(root);
    } else {
      root->right = rightRotate(root->right);
      return leftRotate(root);
    }
  }
  return root;
}

// Print the tree
void printTree(Node *root, string indent, bool last) {
  if (root != nullptr) {
    cout << indent;
    if (last) {
      cout << "R----";
      indent += "   ";
    } else {
      cout << "L----";
      indent += "|  ";
    }
    cout << root->key << endl;
    printTree(root->left, indent, false);
    printTree(root->right, indent, true);
  }
}

int main() {
  Node *root = NULL;
  root = insertNode(root, 33);
  root = insertNode(root, 13);
  root = insertNode(root, 53);
  root = insertNode(root, 9);
  root = insertNode(root, 21);
  root = insertNode(root, 61);
  root = insertNode(root, 8);
  root = insertNode(root, 11);
  printTree(root, "", true);
  root = deleteNode(root, 13);
  cout << "After deleting " << endl;
  printTree(root, "", true);
}

Complexities of Different Operations on an AVL Tree

Insertion	Deletion	Search
O(log n)	O(log n)	O(log n)

AVL Tree Applications

For indexing large records in databases
For searching in large databases

Definition
Balance Factor
Rotating the subtrees in an AVL Tree
Algorithm to Insert a newNode
Algorithm to Delete a node
Python, Java and C/C++ Examples
Complexities of Different Operations on an AVL Tree
AVL Tree Applications

Our premium learning platform, created with over a decade of experience and thousands of feedbacks.

Learn and improve your coding skills like never before.

Try Programiz PRO

Interactive Courses
Certificates
AI Help
2000+ Challenges

Popular Tutorials

Popular Examples

Reference Materials

Certification Courses

Become a certified Python
programmer.

Popular Tutorials

Reference Materials

Popular Examples

DSA Introduction

Data Structures (I)

Data Structures (II)

Tree based DSA (I)

Tree based DSA (II)

Graph based DSA

Sorting and Searching Algorithms

Greedy Algorithms

Dynamic Programming

Other Algorithms

AVL Tree

Balance Factor

Operations on an AVL tree

Rotating the subtrees in an AVL Tree

Left Rotate

Right Rotate

Left-Right and Right-Left Rotate

Algorithm to insert a newNode

Algorithm to Delete a node

Python, Java and C/C++ Examples

Complexities of Different Operations on an AVL Tree

AVL Tree Applications

Table of Contents

Popular Tutorials

Popular Examples

Reference Materials

Certification Courses

Become a certified Python programmer.

Popular Tutorials

Reference Materials

Popular Examples

DSA Introduction

Data Structures (I)

Data Structures (II)

Tree based DSA (I)

Tree based DSA (II)

Graph based DSA

Sorting and Searching Algorithms

Greedy Algorithms

Dynamic Programming

Other Algorithms

DSA Tutorials

AVL Tree

Balance Factor

Operations on an AVL tree

Rotating the subtrees in an AVL Tree

Left Rotate

Right Rotate

Left-Right and Right-Left Rotate

Algorithm to insert a newNode

Algorithm to Delete a node

Python, Java and C/C++ Examples

Complexities of Different Operations on an AVL Tree

AVL Tree Applications

Table of Contents

Related Tutorials

Become a certified Python
programmer.