Certification Courses

Created with over a decade of experience and thousands of feedback.

Learn Python

Learn HTML

Learn JavaScript

Learn SQL

Learn DSA

View all Courses on

Learn C

Learn C++

Learn Java

Red-Black Tree

Red-Black tree is a self-balancing binary search tree in which each node contains an extra bit for denoting the color of the node, either red or black.

A red-black tree satisfies the following properties:

Red/Black Property: Every node is colored, either red or black.
Root Property: The root is black.
Leaf Property: Every leaf (NIL) is black.
Red Property: If a red node has children then, the children are always black.
Depth Property: For each node, any simple path from this node to any of its descendant leaf has the same black-depth (the number of black nodes).

An example of a red-black tree is:

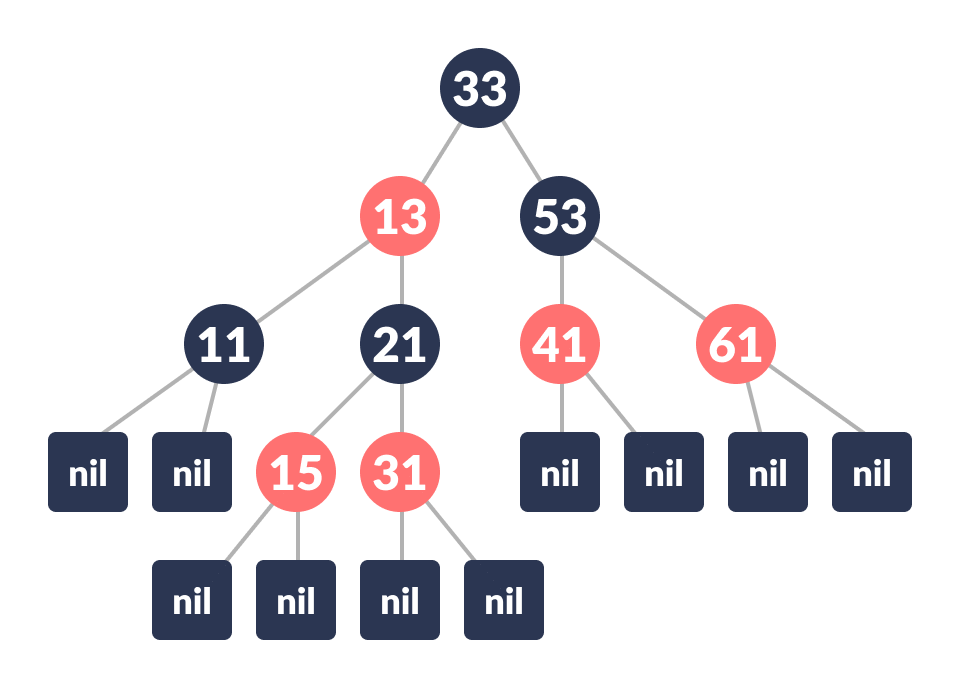
Each node has the following attributes:

color
key
leftChild
rightChild
parent (except root node)

How the red-black tree maintains the property of self-balancing?

The red-black color is meant for balancing the tree.

The limitations put on the node colors ensure that any simple path from the root to a leaf is not more than twice as long as any other such path. It helps in maintaining the self-balancing property of the red-black tree.

Operations on a Red-Black Tree

Various operations that can be performed on a red-black tree are:

Rotating the subtrees in a Red-Black Tree

In rotation operation, the positions of the nodes of a subtree are interchanged.

Rotation operation is used for maintaining the properties of a red-black tree when they are violated by other operations such as insertion and deletion.

There are two types of rotations:

Left Rotate

In left-rotation, the arrangement of the nodes on the right is transformed into the arrangements on the left node.

Algorithm

Let the initial tree be:

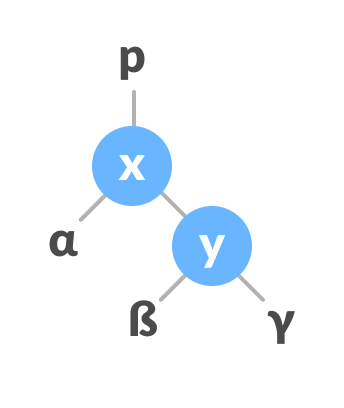
Initial tree
If y has a left subtree, assign x as the parent of the left subtree of y.

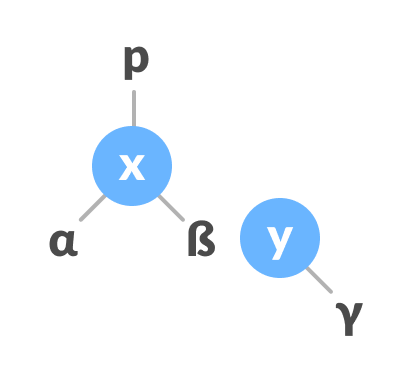
Assign x as the parent of the left subtree of y
If the parent of x is NULL, make y as the root of the tree.
Else if x is the left child of p, make y as the left child of p.
Else assign y as the right child of p.

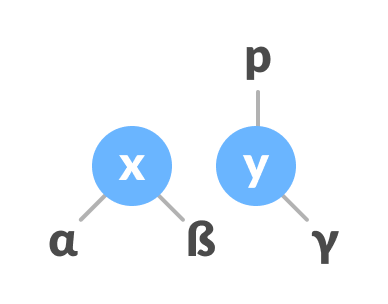
Change the parent of x to that of y
Make y as the parent of x.

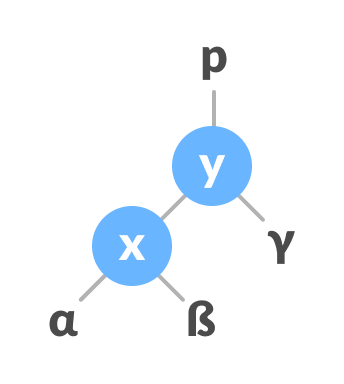
Assign y as the parent of x.

Right Rotate

In right-rotation, the arrangement of the nodes on the left is transformed into the arrangements on the right node.

Let the initial tree be:

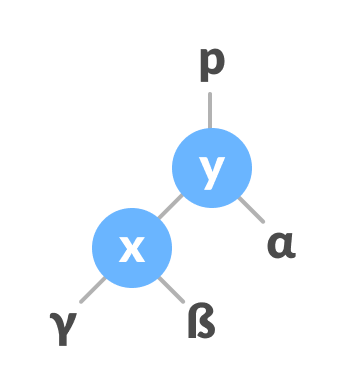
Initial Tree
If x has a right subtree, assign y as the parent of the right subtree of x.

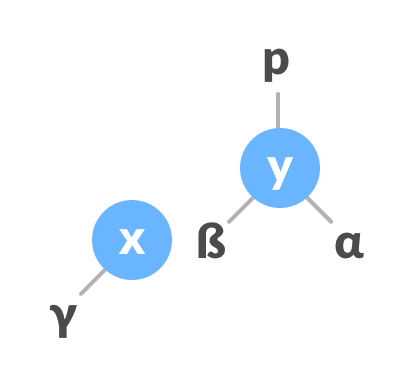
Assign y as the parent of the right subtree of x
If the parent of y is NULL, make x as the root of the tree.
Else if y is the right child of its parent p, make x as the right child of p.
Else assign x as the left child of p.

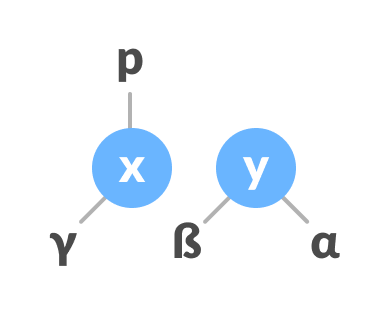
Assign the parent of y as the parent of x
Make x as the parent of y.

Assign x as the parent of y

Left-Right and Right-Left Rotate

In left-right rotation, the arrangements are first shifted to the left and then to the right.

Do left rotation on x-y.

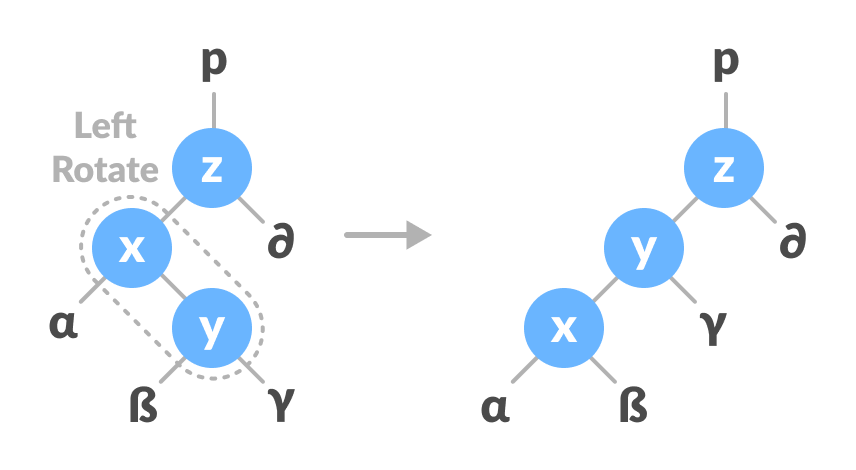
Left rotate x-y
Do right rotation on y-z.

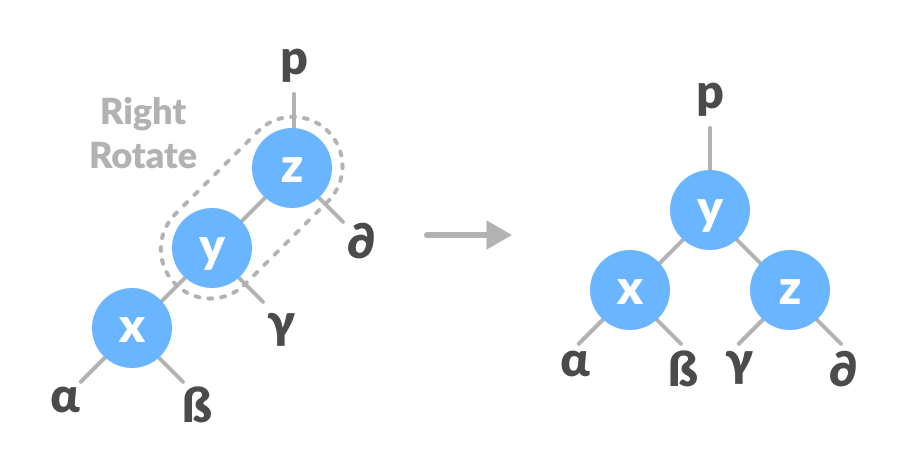
Right rotate z-y

In right-left rotation, the arrangements are first shifted to the right and then to the left.

Do right rotation on x-y.

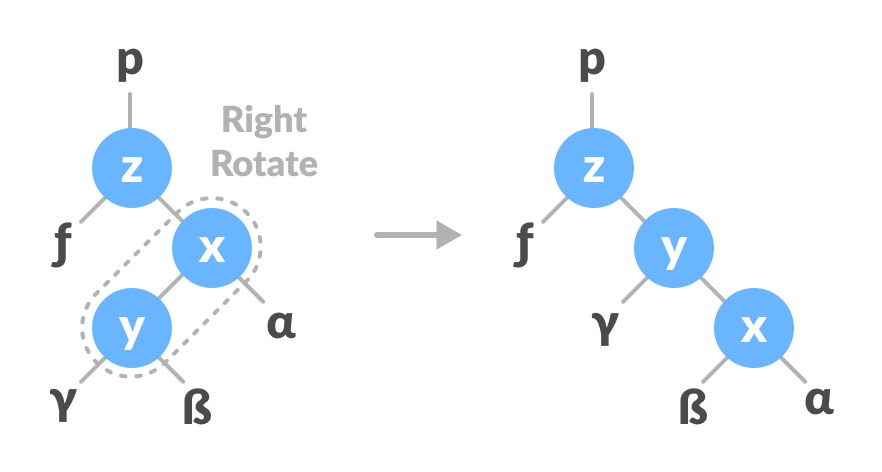
Right rotate x-y
Do left rotation on z-y.

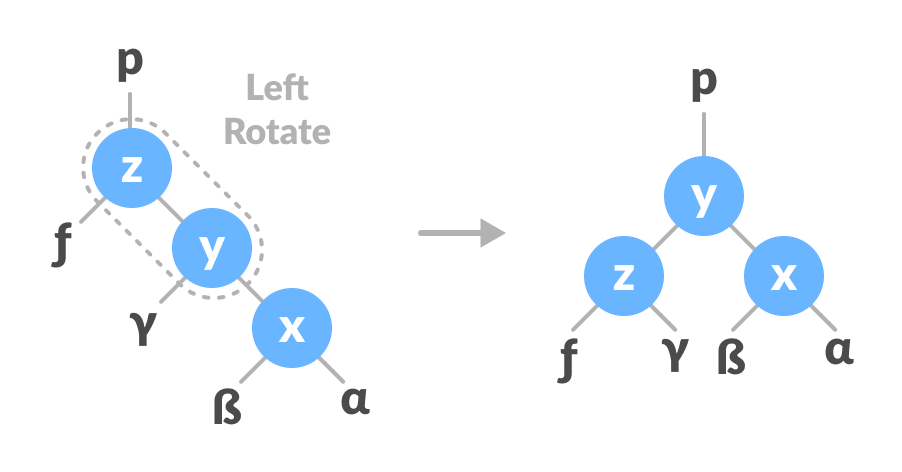
Left rotate z-y

Inserting an element into a Red-Black Tree

While inserting a new node, the new node is always inserted as a RED node. After insertion of a new node, if the tree is violating the properties of the red-black tree then, we do the following operations.

Recolor
Rotation

Algorithm to insert a node

Following steps are followed for inserting a new element into a red-black tree:

Let y be the leaf (ie. NIL) and x be the root of the tree.
Check if the tree is empty (ie. whether x is NIL). If yes, insert newNode as a root node and color it black.
Else, repeat steps following steps until leaf (NIL) is reached.
1. Compare newKey with rootKey.
2. If newKey is greater than rootKey, traverse through the right subtree.
3. Else traverse through the left subtree.
Assign the parent of the leaf as a parent of newNode.
If leafKey is greater than newKey, make newNode as rightChild.
Else, make newNode as leftChild.
Assign NULL to the left and rightChild of newNode.
Assign RED color to newNode.
Call InsertFix-algorithm to maintain the property of red-black tree if violated.

Why newly inserted nodes are always red in a red-black tree?

This is because inserting a red node does not violate the depth property of a red-black tree.

If you attach a red node to a red node, then the rule is violated but it is easier to fix this problem than the problem introduced by violating the depth property.

Algorithm to maintain red-black property after insertion

This algorithm is used for maintaining the property of a red-black tree if the insertion of a newNode violates this property.

Do the following while the parent of newNode p is RED.
If p is the left child of grandParent gP of z, do the following.
Case-I:
1. If the color of the right child of gP of z is RED, set the color of both the children of gP as BLACK and the color of gP as RED.
2. Assign gP to newNode.
  Case-II:
3. Else if newNode is the right child of p then, assign p to newNode.
4. Left-Rotate newNode.
  Case-III:
5. Set color of p as BLACK and color of gP as RED.
6. Right-Rotate gP.
Else, do the following.
1. If the color of the left child of gP of z is RED, set the color of both the children of gP as BLACK and the color of gP as RED.
2. Assign gP to newNode.
3. Else if newNode is the left child of p then, assign p to newNode and Right-Rotate newNode.
4. Set color of p as BLACK and color of gP as RED.
5. Left-Rotate gP.
Set the root of the tree as BLACK.

Deleting an element from a Red-Black Tree

This operation removes a node from the tree. After deleting a node, the red-black property is maintained again.

Algorithm to delete a node

Save the color of nodeToBeDeleted in origrinalColor.
If the left child of nodeToBeDeleted is NULL
1. Assign the right child of nodeToBeDeleted to x.
2. Transplant nodeToBeDeleted with x.
Else if the right child of nodeToBeDeleted is NULL
1. Assign the left child of nodeToBeDeleted into x.
2. Transplant nodeToBeDeleted with x.
Else
1. Assign the minimum of right subtree of noteToBeDeleted into y.
2. Save the color of y in originalColor.
3. Assign the rightChild of y into x.
4. If y is a child of nodeToBeDeleted, then set the parent of x as y.
5. Else, transplant y with rightChild of y.
6. Transplant nodeToBeDeleted with y.
7. Set the color of y with originalColor.
If the originalColor is BLACK, call DeleteFix(x).

Algorithm to maintain Red-Black property after deletion

This algorithm is implemented when a black node is deleted because it violates the black depth property of the red-black tree.

This violation is corrected by assuming that node x (which is occupying y's original position) has an extra black. This makes node x neither red nor black. It is either doubly black or black-and-red. This violates the red-black properties.

However, the color attribute of x is not changed rather the extra black is represented in x's pointing to the node.

The extra black can be removed if

It reaches the root node.
If x points to a red-black node. In this case, x is colored black.
Suitable rotations and recoloring are performed.

The following algorithm retains the properties of a red-black tree.

Do the following until the x is not the root of the tree and the color of x is BLACK
If x is the left child of its parent then,
1. Assign w to the sibling of x.
2. If the right child of parent of x is RED,
  Case-I:
  1. Set the color of the right child of the parent of x as BLACK.
  2. Set the color of the parent of x as RED.
  3. Left-Rotate the parent of x.
  4. Assign the rightChild of the parent of x to w.
3. If the color of both the right and the leftChild of w is BLACK,
  Case-II:
  1. Set the color of w as RED
  2. Assign the parent of x to x.
4. Else if the color of the rightChild of w is BLACK
  Case-III:
  1. Set the color of the leftChild of w as BLACK
  2. Set the color of w as RED
  3. Right-Rotate w.
  4. Assign the rightChild of the parent of x to w.
5. If any of the above cases do not occur, then do the following.
  Case-IV:
  1. Set the color of w as the color of the parent of x.
  2. Set the color of the parent of x as BLACK.
  3. Set the color of the right child of w as BLACK.
  4. Left-Rotate the parent of x.
  5. Set x as the root of the tree.
Else the same as above with right changed to left and vice versa.
Set the color of x as BLACK.

Please refer to insertion and deletion operations for more explanation with examples.

Python, Java and C/C++ Examples

Python

Java

C++

# Implementing Red-Black Tree in Python


import sys


# Node creation
class Node():
    def __init__(self, item):
        self.item = item
        self.parent = None
        self.left = None
        self.right = None
        self.color = 1


class RedBlackTree():
    def __init__(self):
        self.TNULL = Node(0)
        self.TNULL.color = 0
        self.TNULL.left = None
        self.TNULL.right = None
        self.root = self.TNULL

    # Preorder
    def pre_order_helper(self, node):
        if node != TNULL:
            sys.stdout.write(node.item + " ")
            self.pre_order_helper(node.left)
            self.pre_order_helper(node.right)

    # Inorder
    def in_order_helper(self, node):
        if node != TNULL:
            self.in_order_helper(node.left)
            sys.stdout.write(node.item + " ")
            self.in_order_helper(node.right)

    # Postorder
    def post_order_helper(self, node):
        if node != TNULL:
            self.post_order_helper(node.left)
            self.post_order_helper(node.right)
            sys.stdout.write(node.item + " ")

    # Search the tree
    def search_tree_helper(self, node, key):
        if node == TNULL or key == node.item:
            return node

        if key < node.item:
            return self.search_tree_helper(node.left, key)
        return self.search_tree_helper(node.right, key)

    # Balancing the tree after deletion
    def delete_fix(self, x):
        while x != self.root and x.color == 0:
            if x == x.parent.left:
                s = x.parent.right
                if s.color == 1:
                    s.color = 0
                    x.parent.color = 1
                    self.left_rotate(x.parent)
                    s = x.parent.right

                if s.left.color == 0 and s.right.color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.right.color == 0:
                        s.left.color = 0
                        s.color = 1
                        self.right_rotate(s)
                        s = x.parent.right

                    s.color = x.parent.color
                    x.parent.color = 0
                    s.right.color = 0
                    self.left_rotate(x.parent)
                    x = self.root
            else:
                s = x.parent.left
                if s.color == 1:
                    s.color = 0
                    x.parent.color = 1
                    self.right_rotate(x.parent)
                    s = x.parent.left

                if s.right.color == 0 and s.right.color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.left.color == 0:
                        s.right.color = 0
                        s.color = 1
                        self.left_rotate(s)
                        s = x.parent.left

                    s.color = x.parent.color
                    x.parent.color = 0
                    s.left.color = 0
                    self.right_rotate(x.parent)
                    x = self.root
        x.color = 0

    def __rb_transplant(self, u, v):
        if u.parent == None:
            self.root = v
        elif u == u.parent.left:
            u.parent.left = v
        else:
            u.parent.right = v
        v.parent = u.parent

    # Node deletion
    def delete_node_helper(self, node, key):
        z = self.TNULL
        while node != self.TNULL:
            if node.item == key:
                z = node

            if node.item <= key:
                node = node.right
            else:
                node = node.left

        if z == self.TNULL:
            print("Cannot find key in the tree")
            return

        y = z
        y_original_color = y.color
        if z.left == self.TNULL:
            x = z.right
            self.__rb_transplant(z, z.right)
        elif (z.right == self.TNULL):
            x = z.left
            self.__rb_transplant(z, z.left)
        else:
            y = self.minimum(z.right)
            y_original_color = y.color
            x = y.right
            if y.parent == z:
                x.parent = y
            else:
                self.__rb_transplant(y, y.right)
                y.right = z.right
                y.right.parent = y

            self.__rb_transplant(z, y)
            y.left = z.left
            y.left.parent = y
            y.color = z.color
        if y_original_color == 0:
            self.delete_fix(x)

    # Balance the tree after insertion
    def fix_insert(self, k):
        while k.parent.color == 1:
            if k.parent == k.parent.parent.right:
                u = k.parent.parent.left
                if u.color == 1:
                    u.color = 0
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    k = k.parent.parent
                else:
                    if k == k.parent.left:
                        k = k.parent
                        self.right_rotate(k)
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    self.left_rotate(k.parent.parent)
            else:
                u = k.parent.parent.right

                if u.color == 1:
                    u.color = 0
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    k = k.parent.parent
                else:
                    if k == k.parent.right:
                        k = k.parent
                        self.left_rotate(k)
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    self.right_rotate(k.parent.parent)
            if k == self.root:
                break
        self.root.color = 0

    # Printing the tree
    def __print_helper(self, node, indent, last):
        if node != self.TNULL:
            sys.stdout.write(indent)
            if last:
                sys.stdout.write("R----")
                indent += "     "
            else:
                sys.stdout.write("L----")
                indent += "|    "

            s_color = "RED" if node.color == 1 else "BLACK"
            print(str(node.item) + "(" + s_color + ")")
            self.__print_helper(node.left, indent, False)
            self.__print_helper(node.right, indent, True)

    def preorder(self):
        self.pre_order_helper(self.root)

    def inorder(self):
        self.in_order_helper(self.root)

    def postorder(self):
        self.post_order_helper(self.root)

    def searchTree(self, k):
        return self.search_tree_helper(self.root, k)

    def minimum(self, node):
        while node.left != self.TNULL:
            node = node.left
        return node

    def maximum(self, node):
        while node.right != self.TNULL:
            node = node.right
        return node

    def successor(self, x):
        if x.right != self.TNULL:
            return self.minimum(x.right)

        y = x.parent
        while y != self.TNULL and x == y.right:
            x = y
            y = y.parent
        return y

    def predecessor(self,  x):
        if (x.left != self.TNULL):
            return self.maximum(x.left)

        y = x.parent
        while y != self.TNULL and x == y.left:
            x = y
            y = y.parent

        return y

    def left_rotate(self, x):
        y = x.right
        x.right = y.left
        if y.left != self.TNULL:
            y.left.parent = x

        y.parent = x.parent
        if x.parent == None:
            self.root = y
        elif x == x.parent.left:
            x.parent.left = y
        else:
            x.parent.right = y
        y.left = x
        x.parent = y

    def right_rotate(self, x):
        y = x.left
        x.left = y.right
        if y.right != self.TNULL:
            y.right.parent = x

        y.parent = x.parent
        if x.parent == None:
            self.root = y
        elif x == x.parent.right:
            x.parent.right = y
        else:
            x.parent.left = y
        y.right = x
        x.parent = y

    def insert(self, key):
        node = Node(key)
        node.parent = None
        node.item = key
        node.left = self.TNULL
        node.right = self.TNULL
        node.color = 1

        y = None
        x = self.root

        while x != self.TNULL:
            y = x
            if node.item < x.item:
                x = x.left
            else:
                x = x.right

        node.parent = y
        if y == None:
            self.root = node
        elif node.item < y.item:
            y.left = node
        else:
            y.right = node

        if node.parent == None:
            node.color = 0
            return

        if node.parent.parent == None:
            return

        self.fix_insert(node)

    def get_root(self):
        return self.root

    def delete_node(self, item):
        self.delete_node_helper(self.root, item)

    def print_tree(self):
        self.__print_helper(self.root, "", True)


if __name__ == "__main__":
    bst = RedBlackTree()

    bst.insert(55)
    bst.insert(40)
    bst.insert(65)
    bst.insert(60)
    bst.insert(75)
    bst.insert(57)

    bst.print_tree()

    print("\nAfter deleting an element")
    bst.delete_node(40)
    bst.print_tree()

// Implementing Red-Black Tree in Java

class Node {
  int data;
  Node parent;
  Node left;
  Node right;
  int color;
}

public class RedBlackTree {
  private Node root;
  private Node TNULL;

  // Preorder
  private void preOrderHelper(Node node) {
    if (node != TNULL) {
      System.out.print(node.data + " ");
      preOrderHelper(node.left);
      preOrderHelper(node.right);
    }
  }

  // Inorder
  private void inOrderHelper(Node node) {
    if (node != TNULL) {
      inOrderHelper(node.left);
      System.out.print(node.data + " ");
      inOrderHelper(node.right);
    }
  }

  // Post order
  private void postOrderHelper(Node node) {
    if (node != TNULL) {
      postOrderHelper(node.left);
      postOrderHelper(node.right);
      System.out.print(node.data + " ");
    }
  }

  // Search the tree
  private Node searchTreeHelper(Node node, int key) {
    if (node == TNULL || key == node.data) {
      return node;
    }

    if (key < node.data) {
      return searchTreeHelper(node.left, key);
    }
    return searchTreeHelper(node.right, key);
  }

  // Balance the tree after deletion of a node
  private void fixDelete(Node x) {
    Node s;
    while (x != root && x.color == 0) {
      if (x == x.parent.left) {
        s = x.parent.right;
        if (s.color == 1) {
          s.color = 0;
          x.parent.color = 1;
          leftRotate(x.parent);
          s = x.parent.right;
        }

        if (s.left.color == 0 && s.right.color == 0) {
          s.color = 1;
          x = x.parent;
        } else {
          if (s.right.color == 0) {
            s.left.color = 0;
            s.color = 1;
            rightRotate(s);
            s = x.parent.right;
          }

          s.color = x.parent.color;
          x.parent.color = 0;
          s.right.color = 0;
          leftRotate(x.parent);
          x = root;
        }
      } else {
        s = x.parent.left;
        if (s.color == 1) {
          s.color = 0;
          x.parent.color = 1;
          rightRotate(x.parent);
          s = x.parent.left;
        }

        if (s.right.color == 0 && s.right.color == 0) {
          s.color = 1;
          x = x.parent;
        } else {
          if (s.left.color == 0) {
            s.right.color = 0;
            s.color = 1;
            leftRotate(s);
            s = x.parent.left;
          }

          s.color = x.parent.color;
          x.parent.color = 0;
          s.left.color = 0;
          rightRotate(x.parent);
          x = root;
        }
      }
    }
    x.color = 0;
  }

  private void rbTransplant(Node u, Node v) {
    if (u.parent == null) {
      root = v;
    } else if (u == u.parent.left) {
      u.parent.left = v;
    } else {
      u.parent.right = v;
    }
    v.parent = u.parent;
  }

  private void deleteNodeHelper(Node node, int key) {
    Node z = TNULL;
    Node x, y;
    while (node != TNULL) {
      if (node.data == key) {
        z = node;
      }

      if (node.data <= key) {
        node = node.right;
      } else {
        node = node.left;
      }
    }

    if (z == TNULL) {
      System.out.println("Couldn't find key in the tree");
      return;
    }

    y = z;
    int yOriginalColor = y.color;
    if (z.left == TNULL) {
      x = z.right;
      rbTransplant(z, z.right);
    } else if (z.right == TNULL) {
      x = z.left;
      rbTransplant(z, z.left);
    } else {
      y = minimum(z.right);
      yOriginalColor = y.color;
      x = y.right;
      if (y.parent == z) {
        x.parent = y;
      } else {
        rbTransplant(y, y.right);
        y.right = z.right;
        y.right.parent = y;
      }

      rbTransplant(z, y);
      y.left = z.left;
      y.left.parent = y;
      y.color = z.color;
    }
    if (yOriginalColor == 0) {
      fixDelete(x);
    }
  }

  // Balance the node after insertion
  private void fixInsert(Node k) {
    Node u;
    while (k.parent.color == 1) {
      if (k.parent == k.parent.parent.right) {
        u = k.parent.parent.left;
        if (u.color == 1) {
          u.color = 0;
          k.parent.color = 0;
          k.parent.parent.color = 1;
          k = k.parent.parent;
        } else {
          if (k == k.parent.left) {
            k = k.parent;
            rightRotate(k);
          }
          k.parent.color = 0;
          k.parent.parent.color = 1;
          leftRotate(k.parent.parent);
        }
      } else {
        u = k.parent.parent.right;

        if (u.color == 1) {
          u.color = 0;
          k.parent.color = 0;
          k.parent.parent.color = 1;
          k = k.parent.parent;
        } else {
          if (k == k.parent.right) {
            k = k.parent;
            leftRotate(k);
          }
          k.parent.color = 0;
          k.parent.parent.color = 1;
          rightRotate(k.parent.parent);
        }
      }
      if (k == root) {
        break;
      }
    }
    root.color = 0;
  }

  private void printHelper(Node root, String indent, boolean last) {
    if (root != TNULL) {
      System.out.print(indent);
      if (last) {
        System.out.print("R----");
        indent += "   ";
      } else {
        System.out.print("L----");
        indent += "|  ";
      }

      String sColor = root.color == 1 ? "RED" : "BLACK";
      System.out.println(root.data + "(" + sColor + ")");
      printHelper(root.left, indent, false);
      printHelper(root.right, indent, true);
    }
  }

  public RedBlackTree() {
    TNULL = new Node();
    TNULL.color = 0;
    TNULL.left = null;
    TNULL.right = null;
    root = TNULL;
  }

  public void preorder() {
    preOrderHelper(this.root);
  }

  public void inorder() {
    inOrderHelper(this.root);
  }

  public void postorder() {
    postOrderHelper(this.root);
  }

  public Node searchTree(int k) {
    return searchTreeHelper(this.root, k);
  }

  public Node minimum(Node node) {
    while (node.left != TNULL) {
      node = node.left;
    }
    return node;
  }

  public Node maximum(Node node) {
    while (node.right != TNULL) {
      node = node.right;
    }
    return node;
  }

  public Node successor(Node x) {
    if (x.right != TNULL) {
      return minimum(x.right);
    }

    Node y = x.parent;
    while (y != TNULL && x == y.right) {
      x = y;
      y = y.parent;
    }
    return y;
  }

  public Node predecessor(Node x) {
    if (x.left != TNULL) {
      return maximum(x.left);
    }

    Node y = x.parent;
    while (y != TNULL && x == y.left) {
      x = y;
      y = y.parent;
    }

    return y;
  }

  public void leftRotate(Node x) {
    Node y = x.right;
    x.right = y.left;
    if (y.left != TNULL) {
      y.left.parent = x;
    }
    y.parent = x.parent;
    if (x.parent == null) {
      this.root = y;
    } else if (x == x.parent.left) {
      x.parent.left = y;
    } else {
      x.parent.right = y;
    }
    y.left = x;
    x.parent = y;
  }

  public void rightRotate(Node x) {
    Node y = x.left;
    x.left = y.right;
    if (y.right != TNULL) {
      y.right.parent = x;
    }
    y.parent = x.parent;
    if (x.parent == null) {
      this.root = y;
    } else if (x == x.parent.right) {
      x.parent.right = y;
    } else {
      x.parent.left = y;
    }
    y.right = x;
    x.parent = y;
  }

  public void insert(int key) {
    Node node = new Node();
    node.parent = null;
    node.data = key;
    node.left = TNULL;
    node.right = TNULL;
    node.color = 1;

    Node y = null;
    Node x = this.root;

    while (x != TNULL) {
      y = x;
      if (node.data < x.data) {
        x = x.left;
      } else {
        x = x.right;
      }
    }

    node.parent = y;
    if (y == null) {
      root = node;
    } else if (node.data < y.data) {
      y.left = node;
    } else {
      y.right = node;
    }

    if (node.parent == null) {
      node.color = 0;
      return;
    }

    if (node.parent.parent == null) {
      return;
    }

    fixInsert(node);
  }

  public Node getRoot() {
    return this.root;
  }

  public void deleteNode(int data) {
    deleteNodeHelper(this.root, data);
  }

  public void printTree() {
    printHelper(this.root, "", true);
  }

  public static void main(String[] args) {
    RedBlackTree bst = new RedBlackTree();
    bst.insert(55);
    bst.insert(40);
    bst.insert(65);
    bst.insert(60);
    bst.insert(75);
    bst.insert(57);
    bst.printTree();

    System.out.println("\nAfter deleting:");
    bst.deleteNode(40);
    bst.printTree();
  }
}

// Implementing Red-Black Tree in C

#include <stdio.h>
#include <stdlib.h>

enum nodeColor {
  RED,
  BLACK
};

struct rbNode {
  int data, color;
  struct rbNode *link[2];
};

struct rbNode *root = NULL;

// Create a red-black tree
struct rbNode *createNode(int data) {
  struct rbNode *newnode;
  newnode = (struct rbNode *)malloc(sizeof(struct rbNode));
  newnode->data = data;
  newnode->color = RED;
  newnode->link[0] = newnode->link[1] = NULL;
  return newnode;
}

// Insert an node
void insertion(int data) {
  struct rbNode *stack[98], *ptr, *newnode, *xPtr, *yPtr;
  int dir[98], ht = 0, index;
  ptr = root;
  if (!root) {
    root = createNode(data);
    return;
  }

  stack[ht] = root;
  dir[ht++] = 0;
  while (ptr != NULL) {
    if (ptr->data == data) {
      printf("Duplicates Not Allowed!!\n");
      return;
    }
    index = (data - ptr->data) > 0 ? 1 : 0;
    stack[ht] = ptr;
    ptr = ptr->link[index];
    dir[ht++] = index;
  }
  stack[ht - 1]->link[index] = newnode = createNode(data);
  while ((ht >= 3) && (stack[ht - 1]->color == RED)) {
    if (dir[ht - 2] == 0) {
      yPtr = stack[ht - 2]->link[1];
      if (yPtr != NULL && yPtr->color == RED) {
        stack[ht - 2]->color = RED;
        stack[ht - 1]->color = yPtr->color = BLACK;
        ht = ht - 2;
      } else {
        if (dir[ht - 1] == 0) {
          yPtr = stack[ht - 1];
        } else {
          xPtr = stack[ht - 1];
          yPtr = xPtr->link[1];
          xPtr->link[1] = yPtr->link[0];
          yPtr->link[0] = xPtr;
          stack[ht - 2]->link[0] = yPtr;
        }
        xPtr = stack[ht - 2];
        xPtr->color = RED;
        yPtr->color = BLACK;
        xPtr->link[0] = yPtr->link[1];
        yPtr->link[1] = xPtr;
        if (xPtr == root) {
          root = yPtr;
        } else {
          stack[ht - 3]->link[dir[ht - 3]] = yPtr;
        }
        break;
      }
    } else {
      yPtr = stack[ht - 2]->link[0];
      if ((yPtr != NULL) && (yPtr->color == RED)) {
        stack[ht - 2]->color = RED;
        stack[ht - 1]->color = yPtr->color = BLACK;
        ht = ht - 2;
      } else {
        if (dir[ht - 1] == 1) {
          yPtr = stack[ht - 1];
        } else {
          xPtr = stack[ht - 1];
          yPtr = xPtr->link[0];
          xPtr->link[0] = yPtr->link[1];
          yPtr->link[1] = xPtr;
          stack[ht - 2]->link[1] = yPtr;
        }
        xPtr = stack[ht - 2];
        yPtr->color = BLACK;
        xPtr->color = RED;
        xPtr->link[1] = yPtr->link[0];
        yPtr->link[0] = xPtr;
        if (xPtr == root) {
          root = yPtr;
        } else {
          stack[ht - 3]->link[dir[ht - 3]] = yPtr;
        }
        break;
      }
    }
  }
  root->color = BLACK;
}

// Delete a node
void deletion(int data) {
  struct rbNode *stack[98], *ptr, *xPtr, *yPtr;
  struct rbNode *pPtr, *qPtr, *rPtr;
  int dir[98], ht = 0, diff, i;
  enum nodeColor color;

  if (!root) {
    printf("Tree not available\n");
    return;
  }

  ptr = root;
  while (ptr != NULL) {
    if ((data - ptr->data) == 0)
      break;
    diff = (data - ptr->data) > 0 ? 1 : 0;
    stack[ht] = ptr;
    dir[ht++] = diff;
    ptr = ptr->link[diff];
  }

  if (ptr->link[1] == NULL) {
    if ((ptr == root) && (ptr->link[0] == NULL)) {
      free(ptr);
      root = NULL;
    } else if (ptr == root) {
      root = ptr->link[0];
      free(ptr);
    } else {
      stack[ht - 1]->link[dir[ht - 1]] = ptr->link[0];
    }
  } else {
    xPtr = ptr->link[1];
    if (xPtr->link[0] == NULL) {
      xPtr->link[0] = ptr->link[0];
      color = xPtr->color;
      xPtr->color = ptr->color;
      ptr->color = color;

      if (ptr == root) {
        root = xPtr;
      } else {
        stack[ht - 1]->link[dir[ht - 1]] = xPtr;
      }

      dir[ht] = 1;
      stack[ht++] = xPtr;
    } else {
      i = ht++;
      while (1) {
        dir[ht] = 0;
        stack[ht++] = xPtr;
        yPtr = xPtr->link[0];
        if (!yPtr->link[0])
          break;
        xPtr = yPtr;
      }

      dir[i] = 1;
      stack[i] = yPtr;
      if (i > 0)
        stack[i - 1]->link[dir[i - 1]] = yPtr;

      yPtr->link[0] = ptr->link[0];

      xPtr->link[0] = yPtr->link[1];
      yPtr->link[1] = ptr->link[1];

      if (ptr == root) {
        root = yPtr;
      }

      color = yPtr->color;
      yPtr->color = ptr->color;
      ptr->color = color;
    }
  }

  if (ht < 1)
    return;

  if (ptr->color == BLACK) {
    while (1) {
      pPtr = stack[ht - 1]->link[dir[ht - 1]];
      if (pPtr && pPtr->color == RED) {
        pPtr->color = BLACK;
        break;
      }

      if (ht < 2)
        break;

      if (dir[ht - 2] == 0) {
        rPtr = stack[ht - 1]->link[1];

        if (!rPtr)
          break;

        if (rPtr->color == RED) {
          stack[ht - 1]->color = RED;
          rPtr->color = BLACK;
          stack[ht - 1]->link[1] = rPtr->link[0];
          rPtr->link[0] = stack[ht - 1];

          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          dir[ht] = 0;
          stack[ht] = stack[ht - 1];
          stack[ht - 1] = rPtr;
          ht++;

          rPtr = stack[ht - 1]->link[1];
        }

        if ((!rPtr->link[0] || rPtr->link[0]->color == BLACK) &&
          (!rPtr->link[1] || rPtr->link[1]->color == BLACK)) {
          rPtr->color = RED;
        } else {
          if (!rPtr->link[1] || rPtr->link[1]->color == BLACK) {
            qPtr = rPtr->link[0];
            rPtr->color = RED;
            qPtr->color = BLACK;
            rPtr->link[0] = qPtr->link[1];
            qPtr->link[1] = rPtr;
            rPtr = stack[ht - 1]->link[1] = qPtr;
          }
          rPtr->color = stack[ht - 1]->color;
          stack[ht - 1]->color = BLACK;
          rPtr->link[1]->color = BLACK;
          stack[ht - 1]->link[1] = rPtr->link[0];
          rPtr->link[0] = stack[ht - 1];
          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          break;
        }
      } else {
        rPtr = stack[ht - 1]->link[0];
        if (!rPtr)
          break;

        if (rPtr->color == RED) {
          stack[ht - 1]->color = RED;
          rPtr->color = BLACK;
          stack[ht - 1]->link[0] = rPtr->link[1];
          rPtr->link[1] = stack[ht - 1];

          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          dir[ht] = 1;
          stack[ht] = stack[ht - 1];
          stack[ht - 1] = rPtr;
          ht++;

          rPtr = stack[ht - 1]->link[0];
        }
        if ((!rPtr->link[0] || rPtr->link[0]->color == BLACK) &&
          (!rPtr->link[1] || rPtr->link[1]->color == BLACK)) {
          rPtr->color = RED;
        } else {
          if (!rPtr->link[0] || rPtr->link[0]->color == BLACK) {
            qPtr = rPtr->link[1];
            rPtr->color = RED;
            qPtr->color = BLACK;
            rPtr->link[1] = qPtr->link[0];
            qPtr->link[0] = rPtr;
            rPtr = stack[ht - 1]->link[0] = qPtr;
          }
          rPtr->color = stack[ht - 1]->color;
          stack[ht - 1]->color = BLACK;
          rPtr->link[0]->color = BLACK;
          stack[ht - 1]->link[0] = rPtr->link[1];
          rPtr->link[1] = stack[ht - 1];
          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          break;
        }
      }
      ht--;
    }
  }
}

// Print the inorder traversal of the tree
void inorderTraversal(struct rbNode *node) {
  if (node) {
    inorderTraversal(node->link[0]);
    printf("%d  ", node->data);
    inorderTraversal(node->link[1]);
  }
  return;
}

// Driver code
int main() {
  int ch, data;
  while (1) {
    printf("1. Insertion\t2. Deletion\n");
    printf("3. Traverse\t4. Exit");
    printf("\nEnter your choice:");
    scanf("%d", &ch);
    switch (ch) {
      case 1:
        printf("Enter the element to insert:");
        scanf("%d", &data);
        insertion(data);
        break;
      case 2:
        printf("Enter the element to delete:");
        scanf("%d", &data);
        deletion(data);
        break;
      case 3:
        inorderTraversal(root);
        printf("\n");
        break;
      case 4:
        exit(0);
      default:
        printf("Not available\n");
        break;
    }
    printf("\n");
  }
  return 0;
}

// Implementing Red-Black Tree in C++

#include <iostream>
using namespace std;

struct Node {
  int data;
  Node *parent;
  Node *left;
  Node *right;
  int color;
};

typedef Node *NodePtr;

class RedBlackTree {
   private:
  NodePtr root;
  NodePtr TNULL;

  void initializeNULLNode(NodePtr node, NodePtr parent) {
    node->data = 0;
    node->parent = parent;
    node->left = nullptr;
    node->right = nullptr;
    node->color = 0;
  }

  // Preorder
  void preOrderHelper(NodePtr node) {
    if (node != TNULL) {
      cout << node->data << " ";
      preOrderHelper(node->left);
      preOrderHelper(node->right);
    }
  }

  // Inorder
  void inOrderHelper(NodePtr node) {
    if (node != TNULL) {
      inOrderHelper(node->left);
      cout << node->data << " ";
      inOrderHelper(node->right);
    }
  }

  // Post order
  void postOrderHelper(NodePtr node) {
    if (node != TNULL) {
      postOrderHelper(node->left);
      postOrderHelper(node->right);
      cout << node->data << " ";
    }
  }

  NodePtr searchTreeHelper(NodePtr node, int key) {
    if (node == TNULL || key == node->data) {
      return node;
    }

    if (key < node->data) {
      return searchTreeHelper(node->left, key);
    }
    return searchTreeHelper(node->right, key);
  }

  // For balancing the tree after deletion
  void deleteFix(NodePtr x) {
    NodePtr s;
    while (x != root && x->color == 0) {
      if (x == x->parent->left) {
        s = x->parent->right;
        if (s->color == 1) {
          s->color = 0;
          x->parent->color = 1;
          leftRotate(x->parent);
          s = x->parent->right;
        }

        if (s->left->color == 0 && s->right->color == 0) {
          s->color = 1;
          x = x->parent;
        } else {
          if (s->right->color == 0) {
            s->left->color = 0;
            s->color = 1;
            rightRotate(s);
            s = x->parent->right;
          }

          s->color = x->parent->color;
          x->parent->color = 0;
          s->right->color = 0;
          leftRotate(x->parent);
          x = root;
        }
      } else {
        s = x->parent->left;
        if (s->color == 1) {
          s->color = 0;
          x->parent->color = 1;
          rightRotate(x->parent);
          s = x->parent->left;
        }

        if (s->right->color == 0 && s->right->color == 0) {
          s->color = 1;
          x = x->parent;
        } else {
          if (s->left->color == 0) {
            s->right->color = 0;
            s->color = 1;
            leftRotate(s);
            s = x->parent->left;
          }

          s->color = x->parent->color;
          x->parent->color = 0;
          s->left->color = 0;
          rightRotate(x->parent);
          x = root;
        }
      }
    }
    x->color = 0;
  }

  void rbTransplant(NodePtr u, NodePtr v) {
    if (u->parent == nullptr) {
      root = v;
    } else if (u == u->parent->left) {
      u->parent->left = v;
    } else {
      u->parent->right = v;
    }
    v->parent = u->parent;
  }

  void deleteNodeHelper(NodePtr node, int key) {
    NodePtr z = TNULL;
    NodePtr x, y;
    while (node != TNULL) {
      if (node->data == key) {
        z = node;
      }

      if (node->data <= key) {
        node = node->right;
      } else {
        node = node->left;
      }
    }

    if (z == TNULL) {
      cout << "Key not found in the tree" << endl;
      return;
    }

    y = z;
    int y_original_color = y->color;
    if (z->left == TNULL) {
      x = z->right;
      rbTransplant(z, z->right);
    } else if (z->right == TNULL) {
      x = z->left;
      rbTransplant(z, z->left);
    } else {
      y = minimum(z->right);
      y_original_color = y->color;
      x = y->right;
      if (y->parent == z) {
        x->parent = y;
      } else {
        rbTransplant(y, y->right);
        y->right = z->right;
        y->right->parent = y;
      }

      rbTransplant(z, y);
      y->left = z->left;
      y->left->parent = y;
      y->color = z->color;
    }
    delete z;
    if (y_original_color == 0) {
      deleteFix(x);
    }
  }

  // For balancing the tree after insertion
  void insertFix(NodePtr k) {
    NodePtr u;
    while (k->parent->color == 1) {
      if (k->parent == k->parent->parent->right) {
        u = k->parent->parent->left;
        if (u->color == 1) {
          u->color = 0;
          k->parent->color = 0;
          k->parent->parent->color = 1;
          k = k->parent->parent;
        } else {
          if (k == k->parent->left) {
            k = k->parent;
            rightRotate(k);
          }
          k->parent->color = 0;
          k->parent->parent->color = 1;
          leftRotate(k->parent->parent);
        }
      } else {
        u = k->parent->parent->right;

        if (u->color == 1) {
          u->color = 0;
          k->parent->color = 0;
          k->parent->parent->color = 1;
          k = k->parent->parent;
        } else {
          if (k == k->parent->right) {
            k = k->parent;
            leftRotate(k);
          }
          k->parent->color = 0;
          k->parent->parent->color = 1;
          rightRotate(k->parent->parent);
        }
      }
      if (k == root) {
        break;
      }
    }
    root->color = 0;
  }

  void printHelper(NodePtr root, string indent, bool last) {
    if (root != TNULL) {
      cout << indent;
      if (last) {
        cout << "R----";
        indent += "   ";
      } else {
        cout << "L----";
        indent += "|  ";
      }

      string sColor = root->color ? "RED" : "BLACK";
      cout << root->data << "(" << sColor << ")" << endl;
      printHelper(root->left, indent, false);
      printHelper(root->right, indent, true);
    }
  }

   public:
  RedBlackTree() {
    TNULL = new Node;
    TNULL->color = 0;
    TNULL->left = nullptr;
    TNULL->right = nullptr;
    root = TNULL;
  }

  void preorder() {
    preOrderHelper(this->root);
  }

  void inorder() {
    inOrderHelper(this->root);
  }

  void postorder() {
    postOrderHelper(this->root);
  }

  NodePtr searchTree(int k) {
    return searchTreeHelper(this->root, k);
  }

  NodePtr minimum(NodePtr node) {
    while (node->left != TNULL) {
      node = node->left;
    }
    return node;
  }

  NodePtr maximum(NodePtr node) {
    while (node->right != TNULL) {
      node = node->right;
    }
    return node;
  }

  NodePtr successor(NodePtr x) {
    if (x->right != TNULL) {
      return minimum(x->right);
    }

    NodePtr y = x->parent;
    while (y != TNULL && x == y->right) {
      x = y;
      y = y->parent;
    }
    return y;
  }

  NodePtr predecessor(NodePtr x) {
    if (x->left != TNULL) {
      return maximum(x->left);
    }

    NodePtr y = x->parent;
    while (y != TNULL && x == y->left) {
      x = y;
      y = y->parent;
    }

    return y;
  }

  void leftRotate(NodePtr x) {
    NodePtr y = x->right;
    x->right = y->left;
    if (y->left != TNULL) {
      y->left->parent = x;
    }
    y->parent = x->parent;
    if (x->parent == nullptr) {
      this->root = y;
    } else if (x == x->parent->left) {
      x->parent->left = y;
    } else {
      x->parent->right = y;
    }
    y->left = x;
    x->parent = y;
  }

  void rightRotate(NodePtr x) {
    NodePtr y = x->left;
    x->left = y->right;
    if (y->right != TNULL) {
      y->right->parent = x;
    }
    y->parent = x->parent;
    if (x->parent == nullptr) {
      this->root = y;
    } else if (x == x->parent->right) {
      x->parent->right = y;
    } else {
      x->parent->left = y;
    }
    y->right = x;
    x->parent = y;
  }

  // Inserting a node
  void insert(int key) {
    NodePtr node = new Node;
    node->parent = nullptr;
    node->data = key;
    node->left = TNULL;
    node->right = TNULL;
    node->color = 1;

    NodePtr y = nullptr;
    NodePtr x = this->root;

    while (x != TNULL) {
      y = x;
      if (node->data < x->data) {
        x = x->left;
      } else {
        x = x->right;
      }
    }

    node->parent = y;
    if (y == nullptr) {
      root = node;
    } else if (node->data < y->data) {
      y->left = node;
    } else {
      y->right = node;
    }

    if (node->parent == nullptr) {
      node->color = 0;
      return;
    }

    if (node->parent->parent == nullptr) {
      return;
    }

    insertFix(node);
  }

  NodePtr getRoot() {
    return this->root;
  }

  void deleteNode(int data) {
    deleteNodeHelper(this->root, data);
  }

  void printTree() {
    if (root) {
      printHelper(this->root, "", true);
    }
  }
};

int main() {
  RedBlackTree bst;
  bst.insert(55);
  bst.insert(40);
  bst.insert(65);
  bst.insert(60);
  bst.insert(75);
  bst.insert(57);

  bst.printTree();
  cout << endl
     << "After deleting" << endl;
  bst.deleteNode(40);
  bst.printTree();
}

Red-Black Tree Applications

To implement finite maps
To implement Java packages: java.util.TreeMap and java.util.TreeSet
To implement Standard Template Libraries (STL) in C++: multiset, map, multimap
In Linux Kernel

Definition
Rotating the subtrees in a Red-Black Tree
Inserting an element into a Red-Black Tree
Deleting an element from a Red-Black Tree
Python, Java and C/C++ Examples
Red-Black Tree Applications

Previous Tutorial:

Deletion from a B+ tree

Next Tutorial:

Red-Black Tree Insertion

Our premium learning platform, created with over a decade of experience and thousands of feedbacks.

Learn and improve your coding skills like never before.

Try Programiz PRO

Interactive Courses
Certificates
AI Help
2000+ Challenges

Popular Tutorials

Popular Examples

Reference Materials

Certification Courses

Become a certified Python
programmer.

Popular Tutorials

Reference Materials

Popular Examples

DSA Introduction

Data Structures (I)

Data Structures (II)

Tree based DSA (I)

Tree based DSA (II)

Graph based DSA

Sorting and Searching Algorithms

Greedy Algorithms

Dynamic Programming

Other Algorithms

Red-Black Tree

Operations on a Red-Black Tree

Rotating the subtrees in a Red-Black Tree

Left Rotate

Right Rotate

Left-Right and Right-Left Rotate

Inserting an element into a Red-Black Tree

Algorithm to insert a node

Algorithm to maintain red-black property after insertion

Deleting an element from a Red-Black Tree

Algorithm to delete a node

Algorithm to maintain Red-Black property after deletion

Python, Java and C/C++ Examples

Red-Black Tree Applications

Table of Contents

Popular Tutorials

Popular Examples

Reference Materials

Certification Courses

Become a certified Python programmer.

Popular Tutorials

Reference Materials

Popular Examples

DSA Introduction

Data Structures (I)

Data Structures (II)

Tree based DSA (I)

Tree based DSA (II)

Graph based DSA

Sorting and Searching Algorithms

Greedy Algorithms

Dynamic Programming

Other Algorithms

DSA Tutorials

Red-Black Tree

Operations on a Red-Black Tree

Rotating the subtrees in a Red-Black Tree

Left Rotate

Right Rotate

Left-Right and Right-Left Rotate

Inserting an element into a Red-Black Tree

Algorithm to insert a node

Algorithm to maintain red-black property after insertion

Deleting an element from a Red-Black Tree

Algorithm to delete a node

Algorithm to maintain Red-Black property after deletion

Python, Java and C/C++ Examples

Red-Black Tree Applications

Table of Contents

Related Tutorials

Become a certified Python
programmer.