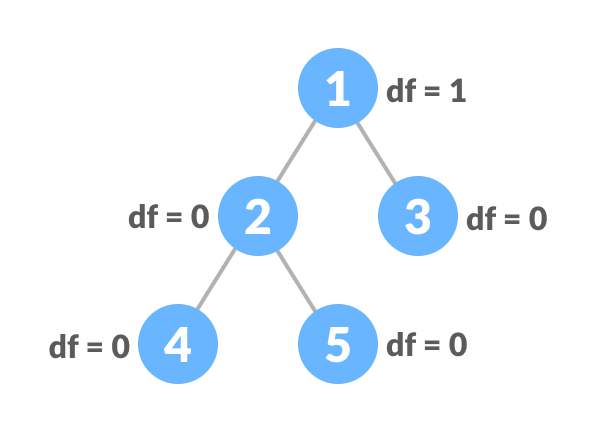
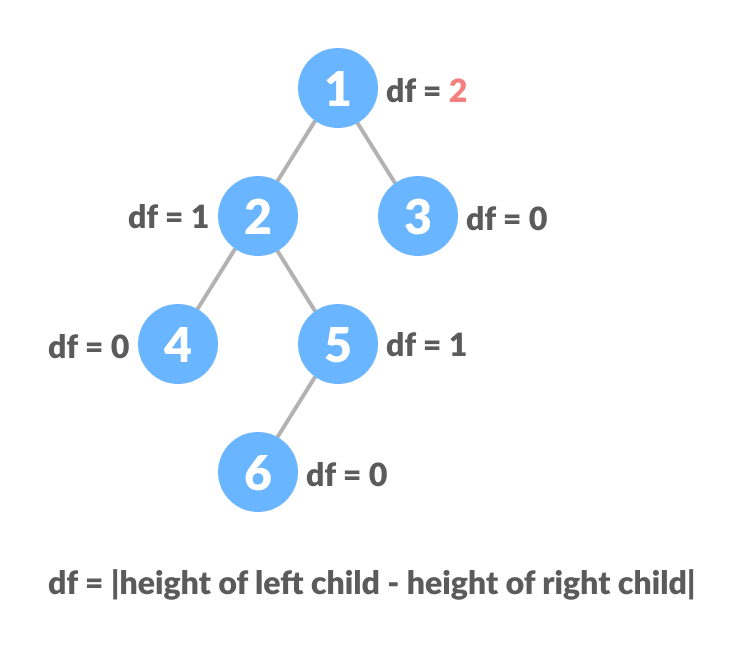
A balanced binary tree, also referred to as a height-balanced binary tree, is defined as a binary tree in which the height of the left and right subtree of any node differ by not more than 1.
To learn more about the height of a tree/node, visit Tree Data Structure. Following are the conditions for a height-balanced binary tree:
- difference between the left and the right subtree for any node is not more than one
- the left subtree is balanced
- the right subtree is balanced
Python, Java and C/C++ Examples
The following code is for checking whether a tree is height-balanced.
# Checking if a binary tree is height balanced in Python
class Node:
def __init__(self, data):
self.data = data
self.left = self.right = None
class Height:
def __init__(self):
self.height = 0
def isHeightBalanced(root, height):
left_height = Height()
right_height = Height()
if root is None:
return True
l = isHeightBalanced(root.left, left_height)
r = isHeightBalanced(root.right, right_height)
height.height = max(left_height.height, right_height.height) + 1
if abs(left_height.height - right_height.height) <= 1:
return l and r
return False
height = Height()
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
if isHeightBalanced(root, height):
print('The tree is balanced')
else:
print('The tree is not balanced')
// Checking if a binary tree is height balanced in Java
// Node creation
class Node {
int data;
Node left, right;
Node(int d) {
data = d;
left = right = null;
}
}
// Calculate height
class Height {
int height = 0;
}
class BinaryTree {
Node root;
// Check height balance
boolean checkHeightBalance(Node root, Height height) {
// Check for emptiness
if (root == null) {
height.height = 0;
return true;
}
Height leftHeighteight = new Height(), rightHeighteight = new Height();
boolean l = checkHeightBalance(root.left, leftHeighteight);
boolean r = checkHeightBalance(root.right, rightHeighteight);
int leftHeight = leftHeighteight.height, rightHeight = rightHeighteight.height;
height.height = (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
if ((leftHeight - rightHeight >= 2) || (rightHeight - leftHeight >= 2))
return false;
else
return l && r;
}
public static void main(String args[]) {
Height height = new Height();
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
if (tree.checkHeightBalance(tree.root, height))
System.out.println("The tree is balanced");
else
System.out.println("The tree is not balanced");
}
}
// Checking if a binary tree is height balanced in C
#include <stdio.h>
#include <stdlib.h>
#define bool int
// Node creation
struct node {
int item;
struct node *left;
struct node *right;
};
// Create a new node
struct node *newNode(int item) {
struct node *node = (struct node *)malloc(sizeof(struct node));
node->item = item;
node->left = NULL;
node->right = NULL;
return (node);
}
// Check for height balance
bool checkHeightBalance(struct node *root, int *height) {
// Check for emptiness
int leftHeight = 0, rightHeight = 0;
int l = 0, r = 0;
if (root == NULL) {
*height = 0;
return 1;
}
l = checkHeightBalance(root->left, &leftHeight);
r = checkHeightBalance(root->right, &rightHeight);
*height = (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
if ((leftHeight - rightHeight >= 2) || (rightHeight - leftHeight >= 2))
return 0;
else
return l && r;
}
int main() {
int height = 0;
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
if (checkHeightBalance(root, &height))
printf("The tree is balanced");
else
printf("The tree is not balanced");
}
// Checking if a binary tree is height balanced in C++
#include
using namespace std;
#define bool int
class node {
public:
int item;
node *left;
node *right;
};
// Create anew node
node *newNode(int item) {
node *Node = new node();
Node->item = item;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
// Check height balance
bool checkHeightBalance(node *root, int *height) {
// Check for emptiness
int leftHeight = 0, rightHeight = 0;
int l = 0, r = 0;
if (root == NULL) {
*height = 0;
return 1;
}
l = checkHeightBalance(root->left, &leftHeight);
r = checkHeightBalance(root->right, &rightHeight);
*height = (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
if (std::abs(leftHeight - rightHeight >= 2))
return 0;
else
return l && r;
}
int main() {
int height = 0;
node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
if (checkHeightBalance(root, &height))
cout << "The tree is balanced";
else
cout << "The tree is not balanced";
}
Balanced Binary Tree Applications
- AVL tree
- Balanced Binary Search Tree